Corpuscule or Wave

September 2, 2022

Throughout the course of human history, the nature of light has been a topic of significant scientific inquiry and philosophical debate. The behavior of light has been studied for many years, but the fundamental properties of light remain uncertain due to the complexity of the phenomenon. Despite centuries of research, the nature of light remains incompletely understood. While there have been significant advances in our understanding of light, there are still many unanswered questions about the nature of light and how it interacts with matter. This article aims to provide a comprehensive overview of our understanding of light up until the year 1900. It will examine the early discoveries and theories related to light and discuss the key scientific advancements that have been made in this field over the years. In the subsequent sections, we will delve deeper into the discovery of the electron and the events that took place during that period. This discovery had a profound impact on our understanding of light and matter and led to significant revisions in the way we think about these concepts. The theoretical catastrophe that occurred in the early 20th century fundamentally altered our understanding of light and the nature of the atom. This event led to the development of new theories and models that better explain the behavior of light and matter. Despite centuries of research, there are still many mysteries surrounding the nature of light that remain unsolved.

1 Introduction
2 Light as waves
3 Light Polarization
4 Luminiferous Ether
5 Photoelectric effect
6 Gas Discharge Tube & Cathode Ray
7 A Catastrophe Is Looming
8 Bibliography

Introduction

The ancient Greeks were renowned for their philosophical inquiry and their study of the natural world. In the field of optics, the Greeks made significant contributions to our understanding of light and vision, which continued during the Hellenistic period through the works of Euclid, Hero of Alexandria, and Ptolemy. Ptolemy’s Optics, in particular, provides a fascinating insight into the philosophical and mathematical foundations of our understanding of light and vision. Ptolemy viewed visual rays as propagating from the eye to the object being observed, which aligns with the ancient Greek belief that the eye was the source of vision. Moreover, Ptolemy’s conception of visual rays forming a continuous cone, rather than Euclid’s proposal of discrete lines, reflects a fundamental shift in our understanding of light and vision. This shift represents a move away from the idea of vision as a passive reception of information to an active process of perception, which involves the interaction of light and the eye. Ptolemy’s experiments on refraction also had significant implications for our understanding of light and the natural world. By discovering that the angle of incidence to the angle of refraction ratio was constant and depended on the properties of the two media, Ptolemy helped to establish the mathematical foundations of optics. In essence, Ptolemy’s work on optics represents a marriage of philosophy, physics, and mathematics. His theories and discoveries reflect the ancient Greek belief in the interconnectedness of all things and the idea that the natural world can be understood through careful observation and inquiry.

In the 5th century BC, Leucippus developed the theory of atomism, which postulated that all matter was composed of small, indivisible particles called atoms. This idea was further developed by Democritus, who expanded on the concept of atomism. However, while atomism held that atoms were uncuttable and indivisible, the corpuscularianism theory allowed corpuscles to be divided. This represented a significant departure from the atomistic view and paved the way for new theories of matter. In the field of optics, Isaac Newton rejected the wave theory of light and developed what is now known as the corpuscular theory of light. According to this theory, light is composed of tiny particles called corpuscles that travel at a finite speed but extremely fast. Newton’s theory gained prominence due to his reputation as a prominent scientist and overtook Huygens’ wave theory of light. Newton’s theory of reflection and refraction attempted to explain the behavior of light when it interacts with different media. He postulated that light accelerates when it enters a denser medium, which explains refraction. Newton also explained diffraction as a result of the ethereal atmosphere near surfaces. However, despite its initial success, the Newtonian theory of light was eventually displaced by the Huygensian theory due to its inability to describe diffraction and interference. The Huygensian theory posits that light is a wave and that it behaves in a manner similar to other types of waves. In summary, the development of the theory of atomism and corpuscularianism represented a significant philosophical and scientific shift in the understanding of matter. Similarly, the corpuscular theory of light put forth by Newton had a significant impact on the field of optics, although it was eventually displaced by the wave theory of light. These developments reflect the ongoing search for a deeper understanding of the natural world and the fundamental building blocks that make up the universe.

The 18th century was a time of significant progress in our understanding of light, with many advances in both theory and practice. One of the most important developments during this time was the proposal of the wave theory of light by Leonhard Euler in 1730. This theory held that light was a wave that traveled through a medium called the “luminiferous ether.” This proposal was a significant departure from the previous corpuscular theory of light, which held that light consisted of tiny particles. Despite the proposal of the wave theory of light, it did not gain widespread acceptance until the 19th century when Thomas Young demonstrated the wave-like properties of light through a series of experiments. Young’s double-slit experiment, in particular, provided compelling evidence for the wave nature of light and helped to solidify the acceptance of the wave theory. During this period, there were also significant advancements in the development of optical instruments. These instruments, such as telescopes and microscopes, relied on the principles of light behavior, such as refraction and reflection, to magnify and observe distant or small objects. The development of these instruments was critical in advancing our understanding of light and its properties. Mathematics played a significant role in the study of light during this time. The wave theory of light, in particular, relied heavily on mathematical models to explain the behavior of light. This theory proposed that light waves had both amplitude and wavelength, and that different colors of light corresponded to different wavelengths. The mathematics of wave theory allowed scientists to develop models that could predict the behavior of light in various situations.

the study of reflection, refraction, and diffraction of light is essential in the field of optics and has led to many important discoveries and advancements. These concepts are fundamental to the development of optical instruments and technologies, and have played a critical role in advancing our understanding of light and its properties. For a deeper understanding of reflection, refraction, and diffraction, please refer to the following information.

Light Reflection

The reflection of light has been a subject of fascination for centuries, inspiring scholars and philosophers to ponder the nature of perception and reality. Hero of Alexandria, a Greek mathematician and engineer who lived in the first century AD, was among the first to formally study the reflection of light. Based on the principle of least distance, Hero derived the law of reflection, which states that the angle of incidence equals the angle of reflection when light reflects off a surface. This law helped to explain the behavior of light when it encounters a reflective surface and provided a foundation for the development of optics. The principle of least distance, upon which Hero based his law of reflection, states that light follows the path of least distance between two points. In other words, when light travels from one point to another, it takes the path that minimizes the distance it has to travel. The law of reflection can be thought of as a special case of the principle of least distance, where the two points are the source of the incoming wavefront and the point of reflection.

At its core, the study of reflection is a study of perception. Our experience of the world is shaped by the way light interacts with objects and surfaces, and the reflection of light plays a critical role in our ability to perceive the world around us. The fact that the angle of incidence equals the angle of reflection suggests that there is a fundamental symmetry to the way light interacts with surfaces. This symmetry is a reflection of the underlying physical laws that govern the behavior of light. The law of reflection also has important implications for the nature of reality. In some ways, the reflection of light can be seen as a metaphor for the way we perceive the world. Just as the reflection of light changes the direction of a wavefront, our perception of reality is shaped by our own biases and perspectives. The image that appears in a mirror is a reflection of reality, but it is also a distortion of reality. In the same way, our perceptions of the world are always filtered through our own subjective experiences and understandings.

The study of reflection is not just a philosophical or conceptual pursuit, however. It is also a deeply mathematical and scientific field. Fermat’s principle of least time, which replaced Hero’s principle of least distance, provides a mathematical framework for understanding the behavior of light as it travels through different media. This principle states that light follows the path of least time, which means that it takes the path that requires the least amount of time to travel between two points. The law of reflection and the principle of least time are fundamental concepts in optics and have been instrumental in the development of technologies such as cameras, telescopes, and microscopes. The principle of least time, which underlies Fermat’s principle, can be understood as follows: when light travels from one point to another, it takes the path that minimizes the time it takes to travel between the two points. In other words, light travels along the path that requires the least amount of time, rather than the shortest distance. This principle provides a more general framework for understanding the behavior of light than the principle of least distance, as it applies to all forms of wave propagation, not just reflection.

Light Refraction

During propagation, waves undergo refraction as they pass from one medium to another. For light propagating from one medium to another, Claudius Ptolemy (100-170 AD) proved that the angle of incidence to refraction was constant and depended on the properties of the mediums.

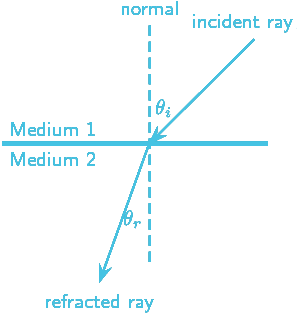
The study of refraction is not just a matter of understanding the physical behavior of light, but also has philosophical implications. The way light refracts as it passes from one medium to another can be seen as a metaphor for the way our perceptions of the world are shaped by our experiences and biases. Just as light is refracted by the properties of the medium it travels through, our perceptions of the world are refracted by the cultural, social, and psychological factors that shape our understanding of reality.

$\theta_{incident} \propto \theta_{refraction}$

According to Snell’s law of refraction (also known as Snell-Descartes and Ibn-Sahl law), light propagates between media that have different refractive indices. There is an inverse relationship between the refractive index of a medium and its light speed. Although Snellius (1580-1626) discovered the law of refraction by trigonometric methods in 1621, Abu Sad Al Alla Ibn Sahl (940-1000) had already discovered it over 600 years earlier.

The mathematical formulation of Snell’s law provides a quantitative description of the relationship between the angle of incidence and the angle of refraction. This relationship can be expressed as:

$\frac{sin(\theta_i)}{sin(\theta_r)}=\frac{v_i}{v_r}=\frac{n_r}{n_i}$

$v$ is velocity and $n$ is the refractive index. $n=c/v$ , where $c$ is the speed of light in a vacuum, which is very close to its speed in air. You can use this lab to do the experiement by your self.

The absolute refractive index n of an optical medium is defined as the ratio of the speed of light in vacuum, $c = 299792458 m/s$ , and the phase velocity v of light in the medium,

$n=\frac{c}{v}$

As an empirical relationship between refractive index and wavelength for a particular transparent medium, the Sellmeier equation can describe the refractive index’s wavelength dependence. This equation was initially proposed by Wolfgang Sellmeier in 1872 and was based on Augustin Cauchy’s equation for modeling dispersion.

$n^2(\lambda) = 1 + \sum_i \frac{B_i \lambda^2}{\lambda^2 - C_i}$

where $n$ is the refractive index, $\lambda$ is the wavelength, and $B_i$ and $C_i$ are experimentally determined Sellmeier coefficients

Derivation of Snell Law

Fermat’s principle states that out of all possible paths that it might take to get from one point to another, light takes the path which requires the shortest time. According to Figure 2 from point A to point B we have

$t=\frac{\sqrt{x^2 + y^2}}{v_i} + \frac{\sqrt{z^2 + (l - x)^2}}{v_r} = \frac{\sqrt{x^2 + y^2}}{v_i} + \frac{\sqrt{z^2 + l^2 -2lx + x^2}}{v_r}$

where $x, y, z$ and l are as denoted in the right-hand figure, $x$ being the varying parameter.

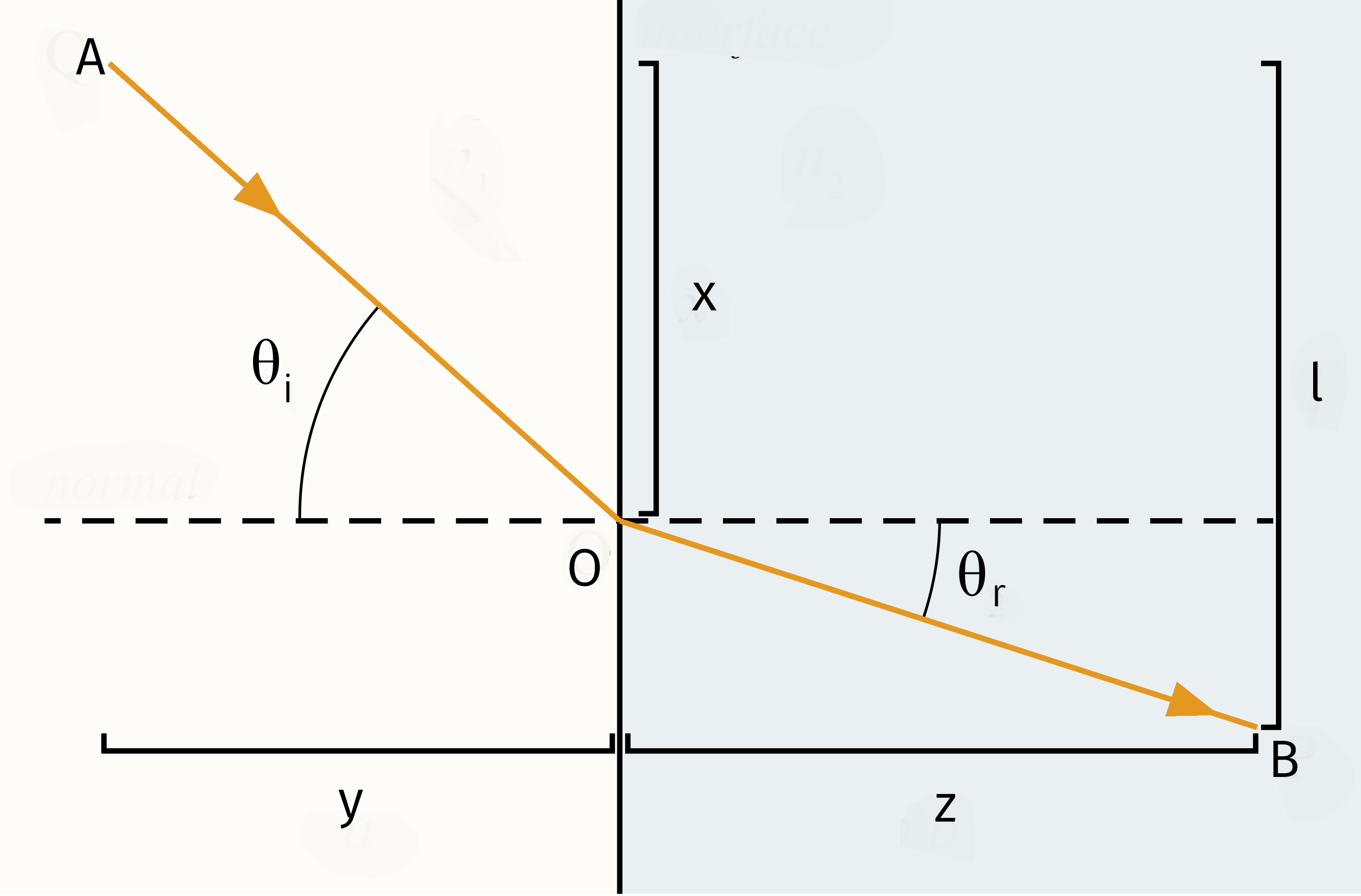
To minimize it, one can differentiate :

$\frac{dt}{dx}=\frac{x}{v_i\sqrt{x^2 + y^2}} + \frac{ - (l - x)}{v_r\sqrt{(l-x)^2 + z^2}}=0$

Based on Figure 2, it can be seen that

$\frac{x}{\sqrt{x^2 + y^2}} =\sin\theta_i$

$\frac{ l - x}{\sqrt{(l-x)^2 + z^2}}=\sin\theta_r$

Therefore,

$\frac{\sin\theta_i}{v_i}=\frac{\sin\theta_r}{v_r}$

$\frac{n_i\sin\theta_i}{c}=\frac{n_r\sin\theta_r}{c}$

$n_i\sin\theta_i=n_r\sin\theta_r$

Light Diffraction

The phenomenon of diffraction, first observed by Francesco Grimaldi (1618–1663), is a crucial aspect of the behavior of light. Through experimentation, Grimaldi showed that light passing through a hole follows a cone-shaped path instead of a rectilinear path that would be expected if light consisted of particles traveling in straight lines. This discovery challenged the prevailing view of light as a collection of discrete particles and paved the way for a deeper understanding of the wave-like nature of light. The study of diffraction has philosophical implications, as it challenges our assumptions about the nature of reality. The fact that light can behave as both a particle and a wave highlights the limitations of our senses and our capacity to comprehend the fundamental nature of the universe. Diffraction forces us to confront the fact that our perceptions of the world are limited by the tools we use to observe it, and that the true nature of reality may be far more complex and mysterious than we can ever hope to understand.

Isaac Newton, one of the most influential scientists of all time, sought to explain the phenomenon of diffraction in terms of his theories of optics. He believed that diffraction was simply a particular case of refraction caused by the ethereal atmosphere near the surface of bodies. However, Newton’s theory was ultimately flawed, as he incorrectly assumed that light accelerated when entering a denser medium due to a stronger gravitational pull. The mathematical principles underlying diffraction are complex and involve the principles of wave interference and diffraction. When light passes through a small opening or aperture, it diffracts, causing the light waves to bend and spread out. The amount of diffraction depends on the size of the aperture and the wavelength of the light. The mathematical formula for calculating the diffraction pattern is known as the Fraunhofer diffraction equation, named after Joseph von Fraunhofer, who made significant contributions to the study of optics in the early 19th century.

The study of diffraction has led to many important discoveries and technological advancements, including the development of X-ray diffraction, which has revolutionized our understanding of the structure of molecules and materials. The phenomenon of diffraction continues to be an active area of research in physics and optics, and its implications for our understanding of the nature of light and the universe are still being explored.

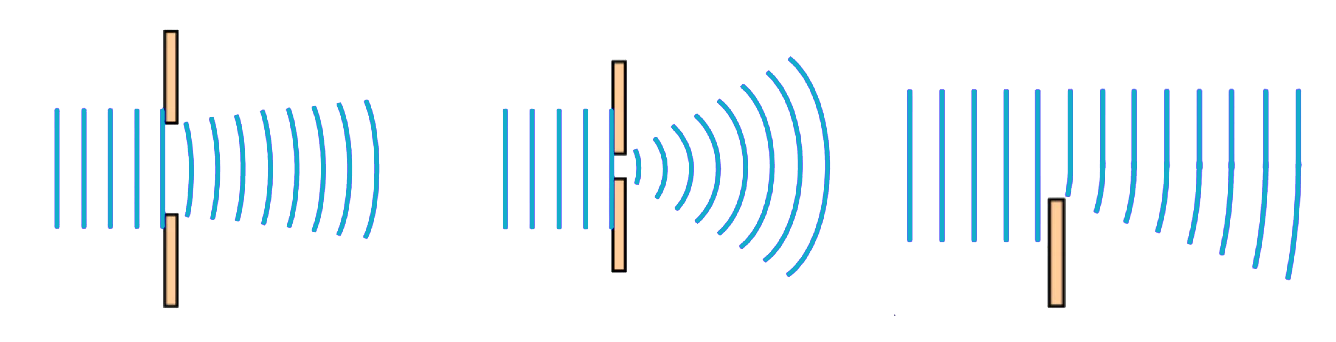
_{Light diffraction through wide and narrow openings as well as around edges.}

Light as waves

Christiaan Huygens’ discovery of the Snell-Descartes law using his wave theory of light in the late 1670s revolutionized our understanding of the nature of light. Huygens’ theory challenged the prevailing view of light as a collection of discrete particles and provided a more comprehensive explanation of the behavior of light. Huygens’ wave theory of light has important philosophical implications, as it challenges our assumptions about the nature of reality. The idea that light is a wave suggests that there is a fundamental interconnectedness of all things in the universe, and that our understanding of the world is limited by our ability to perceive these waves.

Huygens’ wave theory of light postulates that light is disturbed by ether particle vibrations, which propagate through the ether as waves. This concept has important implications for our understanding of the structure of the universe. The idea of an “ether” medium that vibrates to propagate light suggests a fundamental connectedness of all things in the universe. It suggests that there is a fundamental medium that underlies all of reality, and that the vibrations of this medium give rise to the phenomena that we observe.

The wavefront concept that Huygens used to describe his idea of light propagation is a set of particles that are in phase with each other. This means that they are all vibrating in sync, creating a coherent wave. The wavefront concept has important mathematical implications, as it allows us to describe the behavior of light in a more precise and rigorous way. The fact that there is always a 90-degree angle between wavefronts and rays of light is a fundamental aspect of the behavior of light, and has important implications for our understanding of optics and the nature of reality.

Huygens’ preliminary explanation of diffraction was a crucial insight that paved the way for further research in the field. While his ideas were lacking in development and never had formal results, they provided a foundation for future work in this area. The study of diffraction has led to many important discoveries and technological advancements, including the development of X-ray diffraction, which has revolutionized our understanding of the structure of molecules and materials. The study of diffraction and the wave-like nature of light continues to be an active area of research in physics and optics, and has important implications for our understanding of the universe and our place in it. The wave theory of light proposed by Huygens has had a profound impact on our understanding of the nature of light and the universe, and continues to inspire new discoveries and insights today.

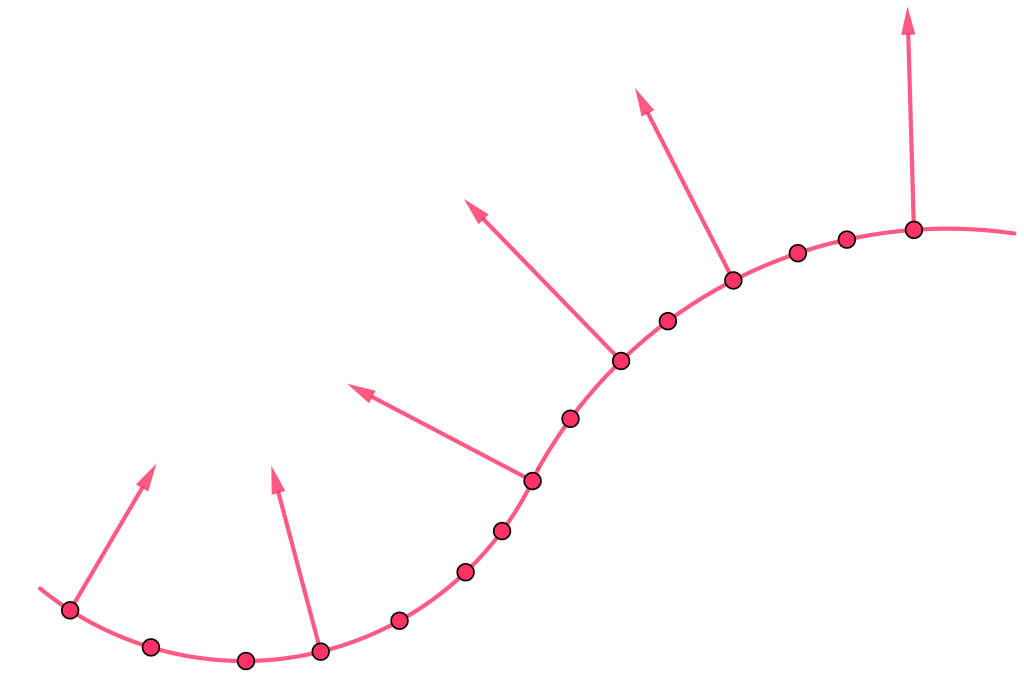
_{There is always a 90-degree angle between wavefronts and rays of light.}

Proof of perpendicularity of rays and wavefronts

The wavefront definition of light propagation is based on the idea that every particle on the wavefront oscillates in sync and must have completed the same number of oscillations. This concept has important mathematical and physical implications, as it allows us to describe the behavior of light in a more precise and rigorous way. However, this definition raises some interesting questions and challenges for our understanding of the nature of light.

Assuming that the particle’s direction is not perpendicular to the wavefront, it has two components: one parallel to the wavefront and the other perpendicular to it. This means that there is a ray traveling along the wavefront, and this ray may not always be perfectly aligned with the wavefront. This has important implications for the behavior of light, as it means that particles on the wavefront may not always oscillate in perfect sync with each other.

For example, consider two points, S and O, very close to each other in a wavefront. If there is a wave traveling from S to O, then S and O could never be in perfect sync with each other because S started oscillating before O. This means that there will be a phase difference between the two particles, even though they are both on the same wavefront. This phase difference can lead to interesting phenomena such as interference and diffraction, which are crucial for understanding the behavior of light.

The wavefront definition of light propagation also has important implications for our understanding of the nature of reality. It suggests that there is a fundamental interconnectedness of all things in the universe, and that the vibrations of the ether medium give rise to the phenomena that we observe. This idea challenges our assumptions about the nature of reality, and suggests that our understanding of the world is limited by our ability to perceive these waves.

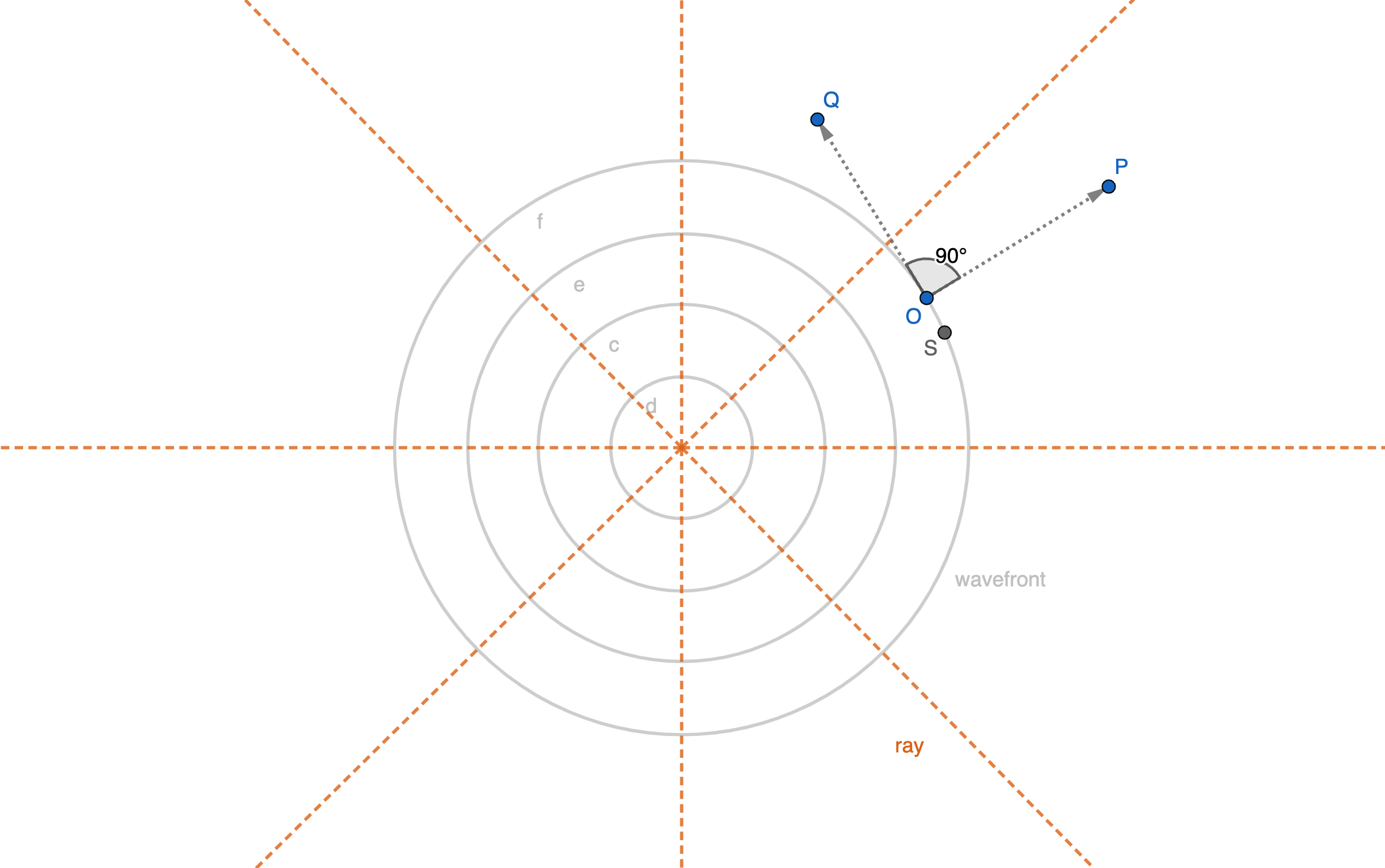
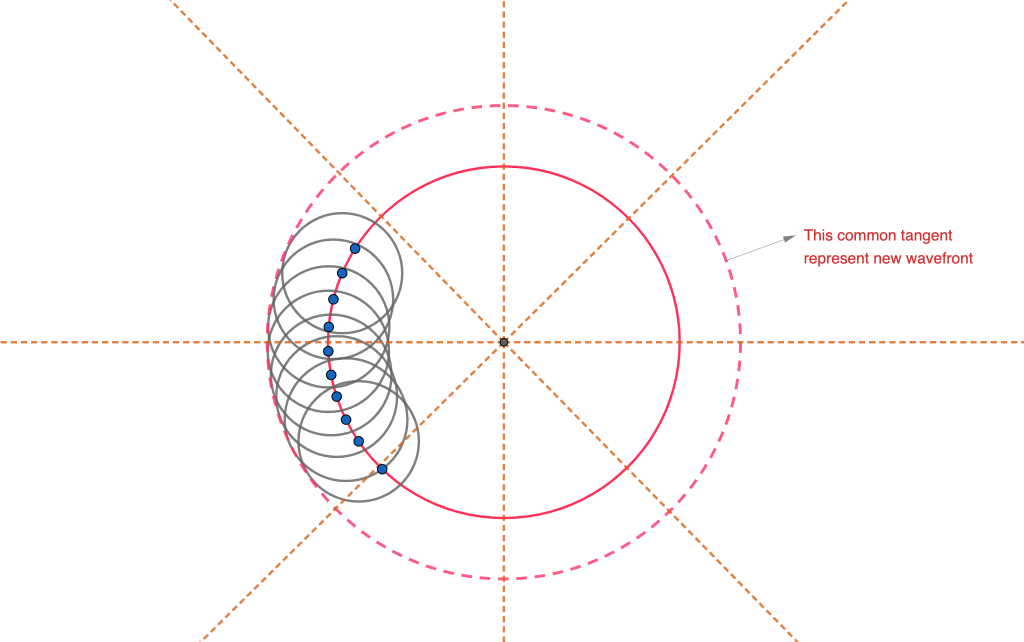
The Huygens hypothesis is a fundamental concept in wave theory, and it provides a powerful tool for describing the behavior of light. According to this hypothesis, every individual point on the wavefront is an ether particle oscillating at the same frequency as the original wave and producing its own spherical waves (secondary waves) as a result. This concept has important mathematical and physical implications, as it allows us to describe the behavior of light in a more precise and rigorous way.

The Huygens hypothesis was a significant development in wave theory, as it challenged the prevailing view of light as a collection of discrete particles. Instead, it proposed that light is a wave that is propagated through the ether medium by the oscillation of individual particles. This idea has important implications for our understanding of the nature of reality, as it suggests that there is a fundamental interconnectedness of all things in the universe.

The secondary waves produced by each individual particle on the wavefront interfere with each other and produce the overall pattern of the wave. This interference can lead to interesting phenomena such as diffraction and interference patterns, which are crucial for understanding the behavior of light. The Huygens hypothesis also has important implications for our understanding of the nature of light and the universe, as it suggests that the vibrations of the ether medium give rise to the phenomena that we observe.

The Huygens hypothesis is a powerful tool for understanding the behavior of light, and it has led to many important discoveries and technological advancements. For example, the study of diffraction and interference patterns has led to the development of technologies such as holography, which has revolutionized our ability to create three-dimensional images. The study of optics and the wave-like nature of light continues to be an active area of research, and has important implications for our understanding of the universe and our place in it.

An example of the application of Huygens principle to the refraction phenomenon can be observed in the figure below.

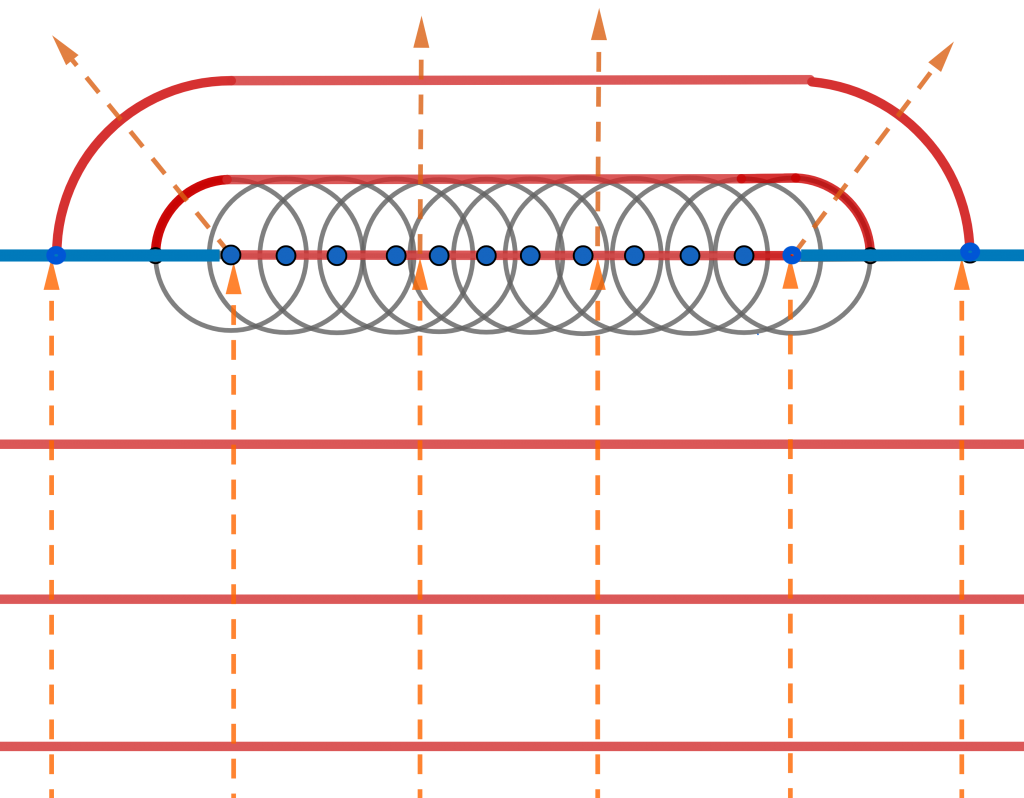
_{Huygen’s principle states that every point on a wavefront behaves as a source for secondary waves, whose common tangent becomes the new wavefront.}

In 1801, Thomas Young published a paper entitled “On the Theory of Light and Colors” that investigated interference phenomena. Two years later, in 1803, he described his famous interference experiment. Although it differs from modern double-slit experiments, it was a crucial step in our understanding of the wave-like nature of light. In his paper, Young proposed that when two undulations from different origins coincide either perfectly or very nearly in direction, their joint effect is a combination of the motions belonging to each. He explained that whenever two portions of the same light arrive at the eye by different routes, either exactly or very nearly in the same direction, the light becomes most intense when the difference of the routes is any multiple of a certain length, and least intense in the intermediate state of the interfering portions. This length is different for light of different colors. Young’s experiment was an early example of the application of Huygens principle, which states that secondary waves travel only in the forward direction. However, the theory did not clarify why this is the case. Huygens was able to explain linear and spherical wave propagation and derive reflection and refraction laws, but he was unable to explain how light deviates from rectilinear propagation at edges.

In 1818, Fresnel restated Huygens’ principle and abolished the corpuscular theory of light until the 20th century. The Fresnel theory was based on wave theory, combining Huygens’ principle and Young’s principle of interference. According to Fresnel, the vibration at any given point on a wavefront is the sum of the vibrations that would be sent to it at that moment by all of the wavefront elements in any previous position, with all elements acting independently. Whenever a wavefront is partly obstructed, the summation should be carried out. Using the Huygens-Fresnel principle, we can explain how these wavefronts evolve in time under every situation, even when obstacles are present. Diffraction was one of the phenomena he could explain using secondary waves. In the following figure, we consider the wavefront in plane form.

The development of the Huygens-Fresnel principle was a significant step in our understanding of the wave-like nature of light. It allowed us to explain a wide range of phenomena, including interference, diffraction, and reflection and refraction at boundaries. These discoveries had important implications for our understanding of the universe and our place in it. Today, the study of optics and the wave-like nature of light continues to be an active area of research, with important implications for a wide range of fields, including telecommunications, medicine, and materials science.

_{It is a line tangent to all of the wavelets that form a wavefront in a plane far from its source. Every point on a wavefront is a source of wavelets.}

Light Polarization

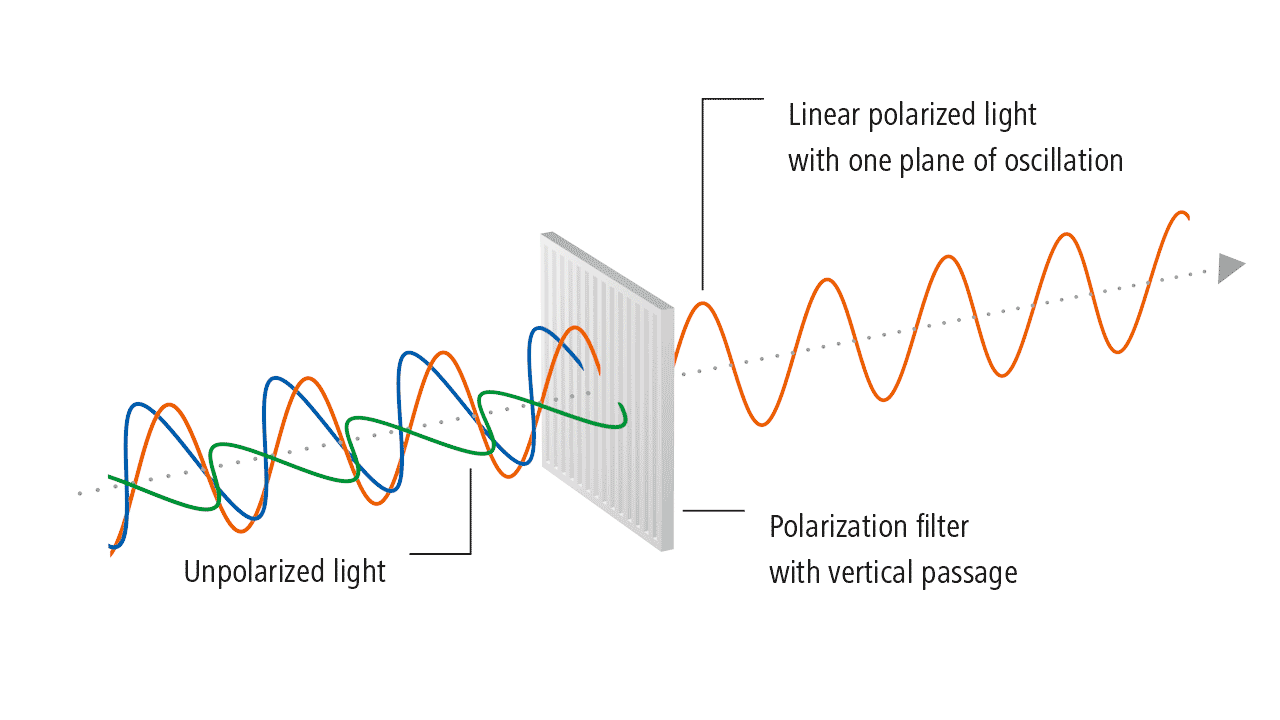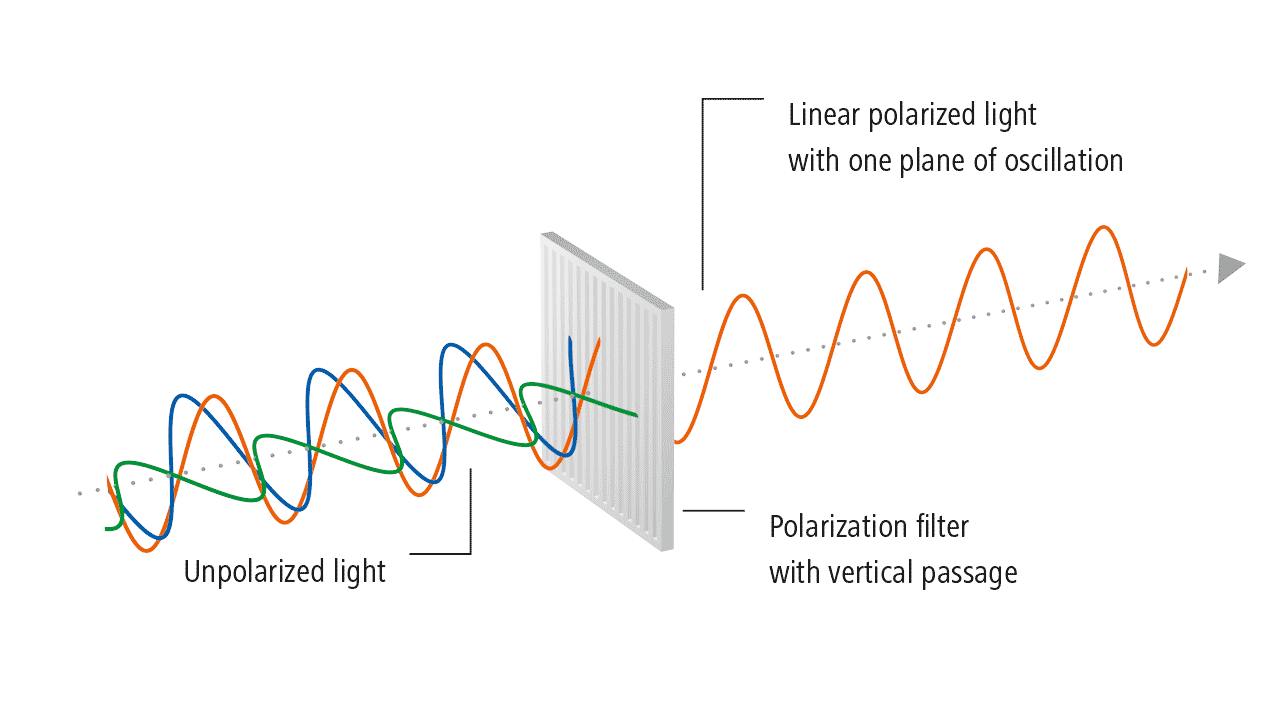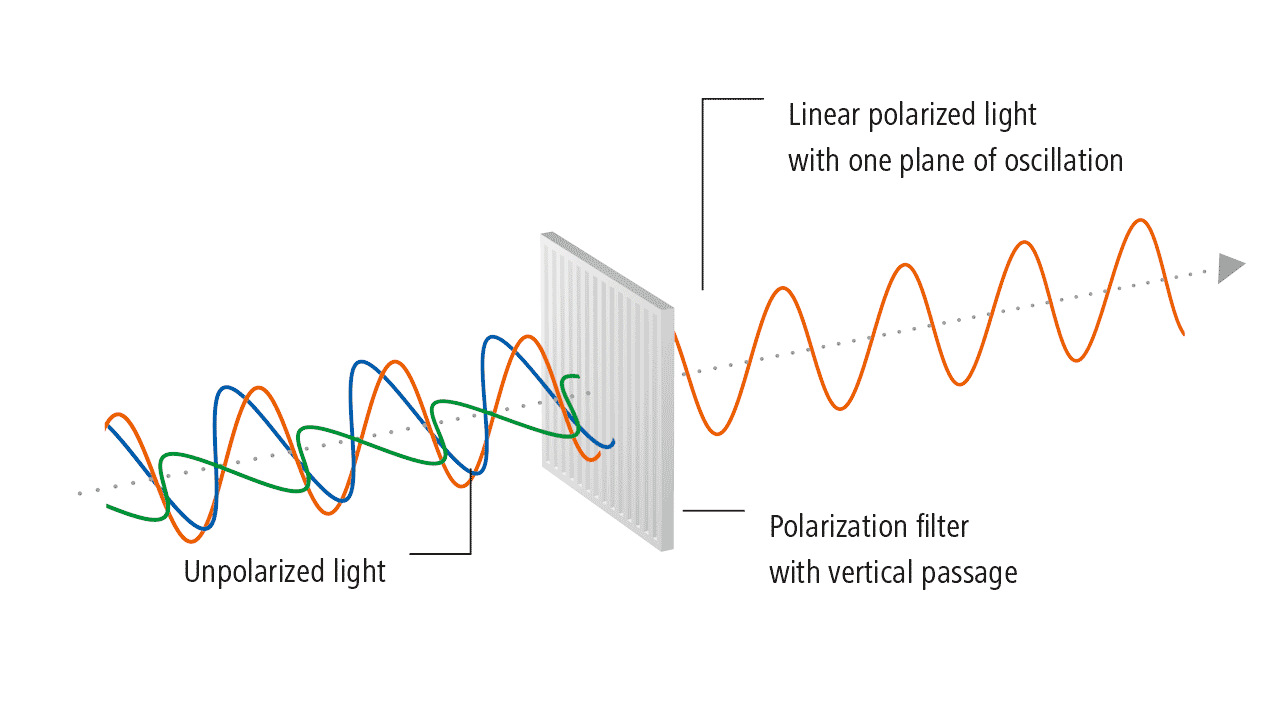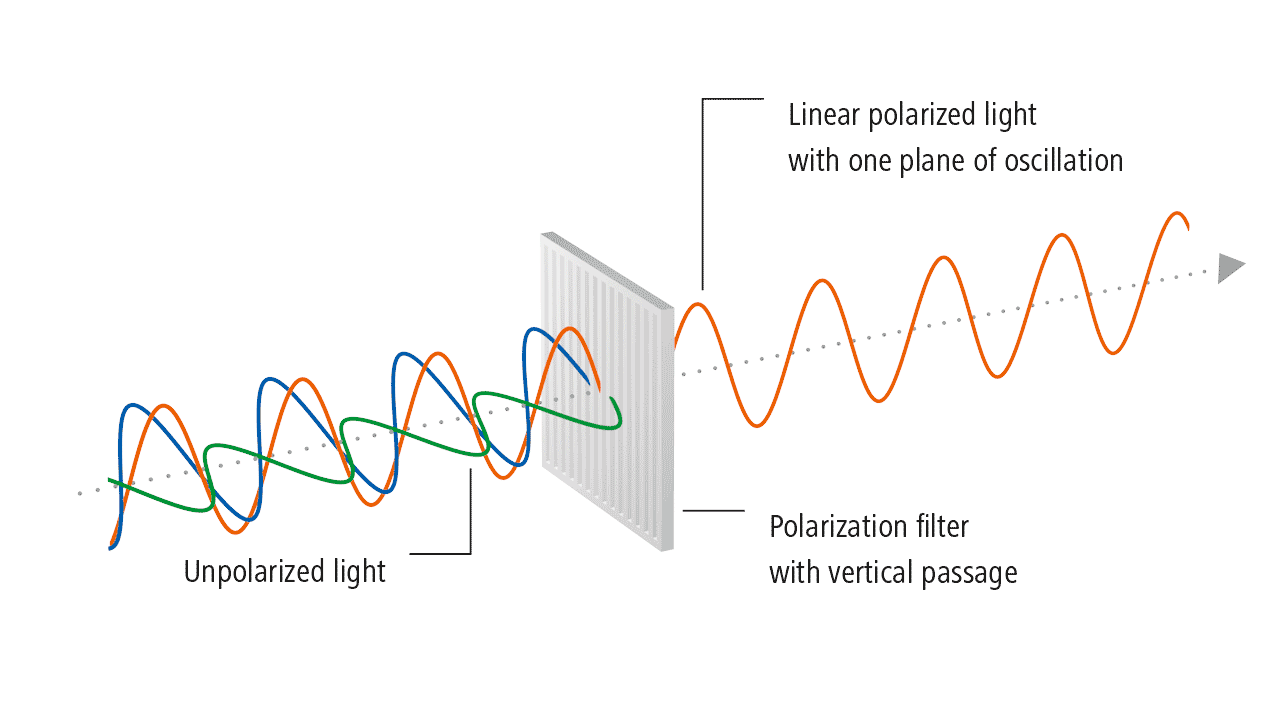
Transverse waves possess the property of polarization, which indicates their geometrical orientation. A transverse wave is a wave whose oscillations are perpendicular to the propagation of light. As opposed to longitudinal waves, which travel in the direction of their oscillations, transverse waves oscillate perpendicular to their motion due to polarization of light. Polarization of light describes the phenomenon of limiting light’s vibration to a particular plane perpendicular to its propagation.(figure 9: source )

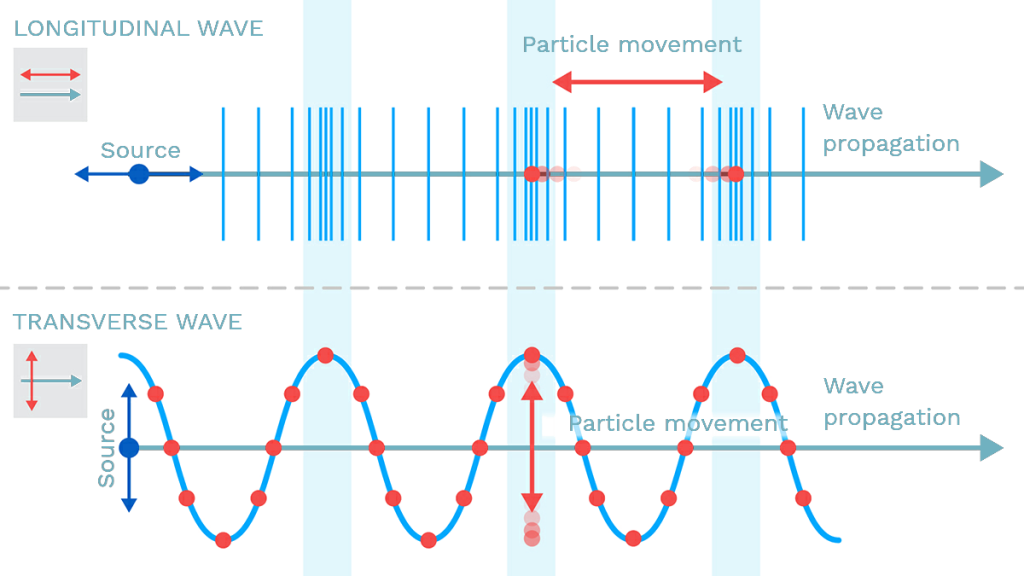
_{Waves can be categorized as either longitudinal or transverse}

The history of light polarization began with Birefringence, which is formally defined as the double refraction of light in a transparent, molecularly ordered material, which is manifested by the existence of orientation-dependent differences in the refractive index. These crystals were first examined by Rasmus Bartholin, who discovered that you can see two images of the object when you look through them. When a narrow beam of light passes through them, a refracted beam is split into two parts that travel through the crystal and emerge as two separate beams. A 60-page pamphlet summarizing his observations, which he could not explain, was published in 1669. In spite of the fact that Bartholin himself was unable to explain double refraction, it was recognized that it was a serious contradiction to Newton’s theories.

According to Huygens’s wave theory, each point on a wavefront becomes a source of new disturbances and sends secondary wavelets. At any given instant, the envelope of the secondary wavelets gives us a new wavefront. In its original form, Huygens’s theory cannot explain double reflection in uniaxial crystals. For this reason, he developed the secondary wavelet theory to explain the phenomenon. The following summarizes only the salient features of his extended approach.

When a wavefront is incident on a doubly refracting crystal, every point on the
crystal becomes the origin of two wavefronts, O-ray and E-ray. One the ordinary and the other extraordinary to account for the two types of rays.
Ordinary wavefront corresponds to the ordinary rays which obey the laws of
refraction and have the same velocity in all directions. The ordinary wavefront is thus spherical
Extraordinary wavefront corresponds to the extraordinary rays which do not
obey the laws of refraction and have different velocities in different directions. The extraordinary wavefront is thus an ellipsoid of revolution, with the optic axis as the axis of revolution.
The sphere and the ellipsoid touch each other at points that lie on the optic axis of the crystal, since the velocity of the ordinary and the extraordinary ray is the sane along the optic axis. So, the uniaxial crystals do not show any double refraction along the optic axis.(Figure below: source )

_{Birefringence according to Huygens’s wave theory.}

While conducting experiments on double refraction, Malus noticed that light from the Luxembourg palace windows reflected through an Iceland spar crystal. He was surprised to find that when he rotated the crystal around the axis of vision, the intensity of the two images varied. He suspected that the reflected rays of light acquired an asymmetry similar to that observed by Huygens for the ordinary and extraordinary rays issuing from a crystal of Iceland spar.He soon found that the analogy was complete when the reflection occurred at a specific incidence, $52^\circ$ in the case of a water surface.

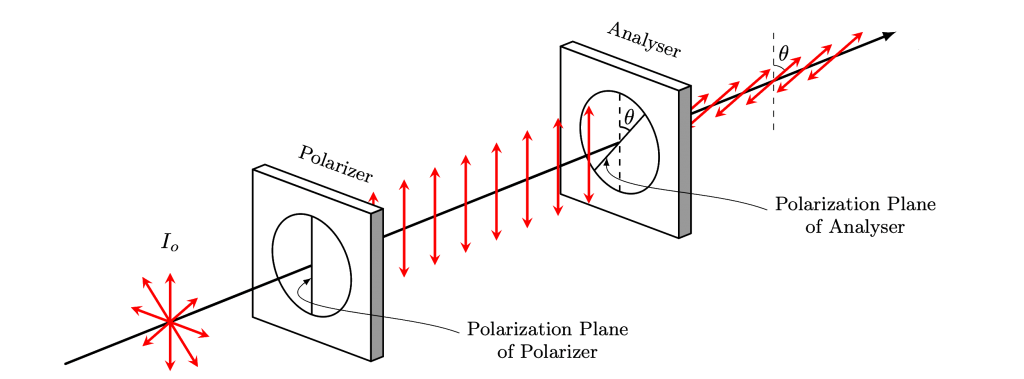
Malus’s law is a fundamental law of optics that describes the relationship between the intensity of polarized light transmitted through a polarizer and the angle between the polarizer and the plane of polarization of the incident light. Mathematically, Malus’s law is expressed as:

(1) $\begin{equation*}I = I_0 \cos^2\theta\end{equation*}$

where $I_0$ is the intensity of the incident light, $\theta$ is the angle between the polarizer and the plane of polarization of the incident light, and $I$ is the transmitted intensity of the polarized light.

The derivation of Malus’s law can be carried out using the principles of wave polarization. When a plane polarized wave is incident on a polarizer, the component of the electric field vector that is parallel to the transmission axis of the polarizer is transmitted, while the component that is perpendicular to the transmission axis is absorbed. As a result, the transmitted wave is polarized in the direction of the transmission axis of the polarizer.

The transmitted wave can be represented mathematically as a vector:

(2) $\begin{equation*}\vec{E}_t = E_0 \cos\theta\hat{x}\end{equation*}$

where $E_0$ is the amplitude of the incident wave, and $\theta$ is the angle between the polarizer and the plane of polarization of the incident wave. The vector $\theta$ is represented by the unit vector $\hat{x}$ .

The intensity of the transmitted wave is given by the magnitude of the Poynting vector, which is defined as the product of the electric field vector and the magnetic field vector divided by the impedance of free space:

(3) $\begin{equation*}I = |\vec{S}| = \frac{1}{\mu_0} |\vec{E}|^2\end{equation*}$

where $\mu_0$ is the permeability of free space.

Substituting the expression for the transmitted electric field vector into the equation for the intensity of the transmitted wave, we obtain:

(4) $\begin{equation*}I = \frac{1}{\mu_0} (E_0 \cos\theta)^2 = I_0 \cos^2\theta\end{equation*}$

where $I_0 = \frac{1}{\mu_0}{E_0}^2$ is the intensity of the incident wave.

Thus, we have derived Malus’s law, which relates the transmitted intensity of polarized light to the angle between the polarizer and the plane of polarization of the incident light.

Malus’s law has significant implications in many areas of science and technology, including optics, telecommunications, and materials science. It has led to the development of various polarizing devices, such as polarizers and waveplates, which are used in numerous applications, including in liquid crystal displays, optical filters, and polarized sunglasses. The law continues to play a critical role in the understanding and manipulation of polarized light and has paved the way for the development of new technologies that utilize the unique properties of polarized light.

Malus’s discovery of polarization and its application to light was a significant milestone in the field of optics. In 1808, Malus used reflection to produce plane polarized light. When an unpolarized light wave is incident on a surface of a transparent medium, some part of the light is reflected and the rest is refracted through the medium. Malus found that as the angle of incidence changes, the degree of polarization of the reflected wave also changes. At a particular angle, the reflected wave becomes completely plane polarized. This angle is known as the Brewster angle or dipolarizing angle.

Brewster subsequently discovered the law that when light is incident at the polarizing angle $\theta_p$ at the interface of a transparent medium, the refractive index of the medium is given by:

$n = \tan \theta_p$

This law is known as Brewster’s law and is a fundamental principle in the study of polarization of light. It relates the angle of incidence at which the reflected ray is completely polarized to the refractive index of the medium. The polarizing angle $\theta_p$ is given by:

$\theta_p = \tan^{-1}(\frac{n_2}{n_1})$

where $n_1$ and $n_2$ are the refractive indices of the incident and refracted media, respectively.

Brewster’s law has significant implications in the study of polarization of light and has led to the development of various polarizing devices, such as polarizers and waveplates, which are used in numerous applications, including in liquid crystal displays, optical filters, and polarized sunglasses. It continues to play a critical role in the understanding and manipulation of polarized light and has paved the way for the development of new technologies that utilize the unique properties of polarized light.

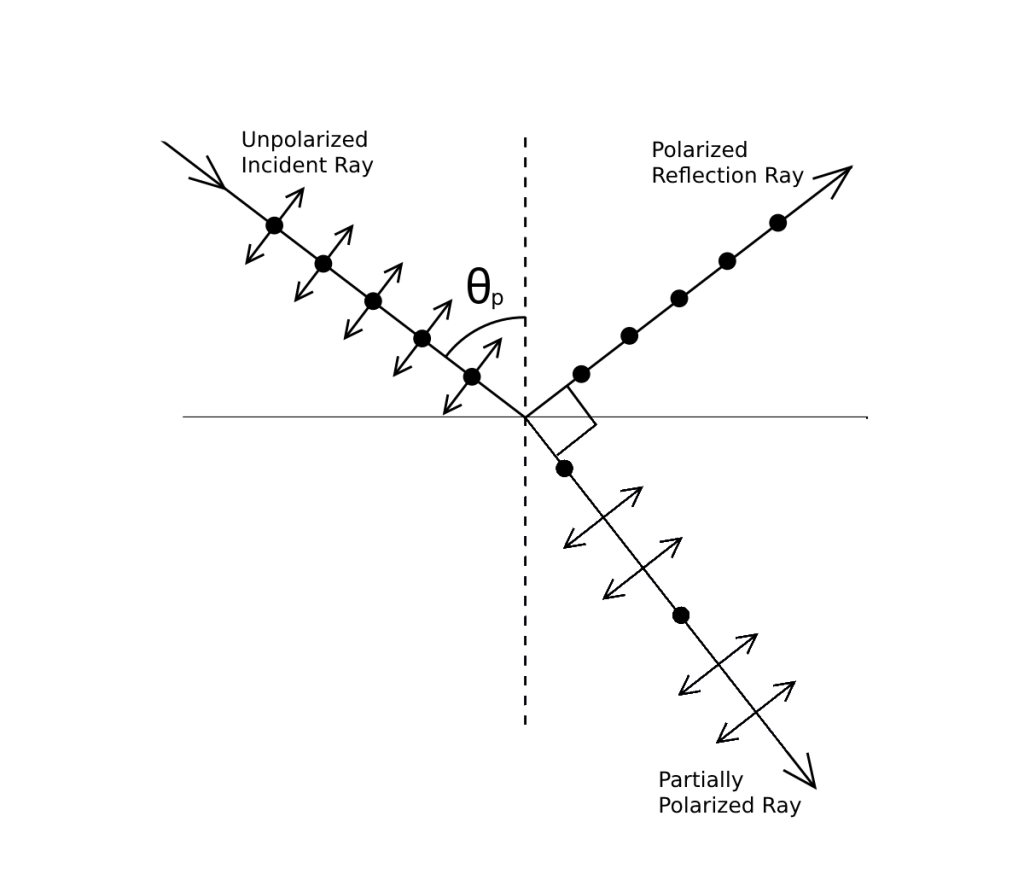
The interference pattern of a double-slit device depends on the polarization of the light. In a more general experiment suggested by Arago, where the two beams were separately polarized, the interference pattern appeared and disappeared as the polarization of one beam was rotated. When the two beams are polarized in parallel directions, interference is complete, whereas in perpendicular polarizations, there is no interference.

To explain these phenomena, Fresnel developed a model of the ether that allowed transverse vibrations but forbade longitudinal vibrations. According to this model, the ether consists of a regular lattice of molecules held in equilibrium by distance forces. Fresnel’s model allowed him to explain the new types of polarization discovered by Biot, Brewster, and himself in reflected light and light transmitted through crystal laminae.

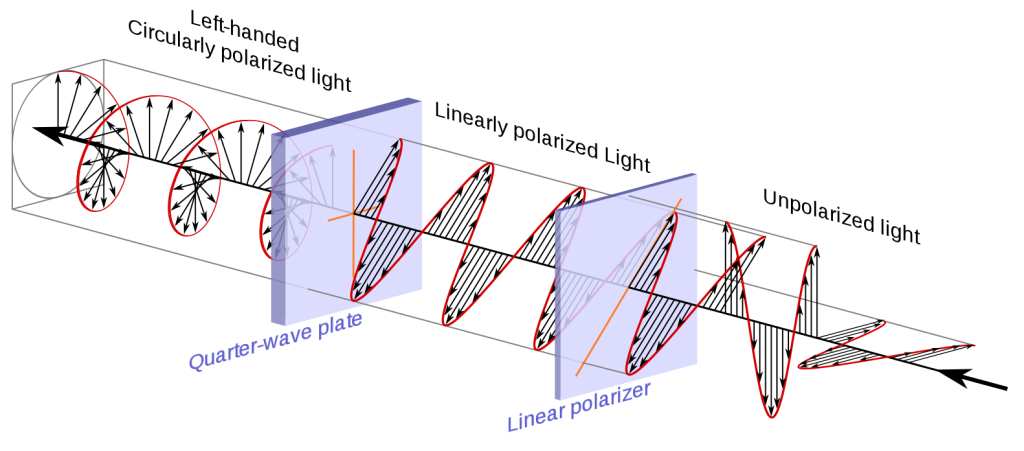
For example, consider a light wave that is polarized rectilinearly and passes through a quarter-wave plate. Quarter-wave plates are made of birefringent materials whose thickness has been carefully adjusted so that light with a larger index of refraction is phase retarded 90° (quarter wavelength) from light with a smaller index. The image intensity of this light is not affected by the azimuth of the analyzer when seen through an analyzer: it behaves as if it were wholly depolarized. The difference between this light and natural light is that it can be made to pass through another quarter-wave plate to become rectilinearly polarized.

Fresnel assumed that the incident wave could always be a superposition of two vibrations, one in the plane of incidence and one perpendicular to it. He further assumed that the elastic constants of the two media were equal and imposed two boundary conditions: the energy of the incoming wave was equal to that of the reflected and refracted waves, and the parallel components of the total vibration on both sides were equal. These assumptions led to Fresnel’s law of tangents, which relates the vibrational amplitude of the incident and reflected waves:

$\frac{a_i}{a_r}=\frac{\tan(i-r)}{\tan(i+r)}$

where $a_i$ and $a_r$ are the vibrational amplitudes of the incident and reflected waves, respectively, and $i$ and $r$ are the angles of incidence and reflection, respectively. Fresnel’s law of tangents is a fundamental principle in the study of polarization of light and has numerous applications in a variety of fields, including optics, physics, and engineering.

Luminiferous Ether

Waves are disturbances that propagate through a medium. For instance, sound waves travel through air, which acts as a medium. If we accept that light behaves as a wave, then it should also require a medium to propagate through. This led to the concept of aether, which is an ancient Greek term that referred to the primordial god of light and the upper air, considered to be the purest and finest air that the gods breathe. Aether was also known as the fifth element, after water, air, fire, and earth, and was believed to fill the region of the universe beyond the sublunary sphere. This idea was followed by Descartes, who believed that forces between bodies not in direct contact were based on an intermediate medium, and that astrological bodies transmitted forces through the aether as flowing in vortices. Huygens mathematically showed that gravity could be described as fluid dynamics of aether.

In Huygens’ wave theory of light, the aether was assumed to be the medium of wave light, and he developed his theory based on this assumption. However, the existence of aether was challenged by the Michelson-Morley experiment in 1887. The experiment was designed to detect the existence of aether by observing the interference pattern between two beams of light, each traveling along different arms of a device called an interferometer. The influence of the “ether wind” was expected to change the time the beams of light traveled along the arms, affecting the interference pattern. The experiment was conducted at different times of day and of the year, but the interference pattern did not change.

This result was a significant blow to the concept of aether as the medium of light waves. However, the interpretation of the Michelson-Morley experiment was not straightforward, and various explanations were proposed to reconcile the results with the wave theory of light. One of the proposed explanations was the Lorentz-Fitzgerald contraction hypothesis, which suggested that objects moving through the aether would contract in the direction of motion, making it impossible to detect the motion of the aether relative to the observer. This hypothesis paved the way for the development of the special theory of relativity by Einstein, which fundamentally changed our understanding of space and time.

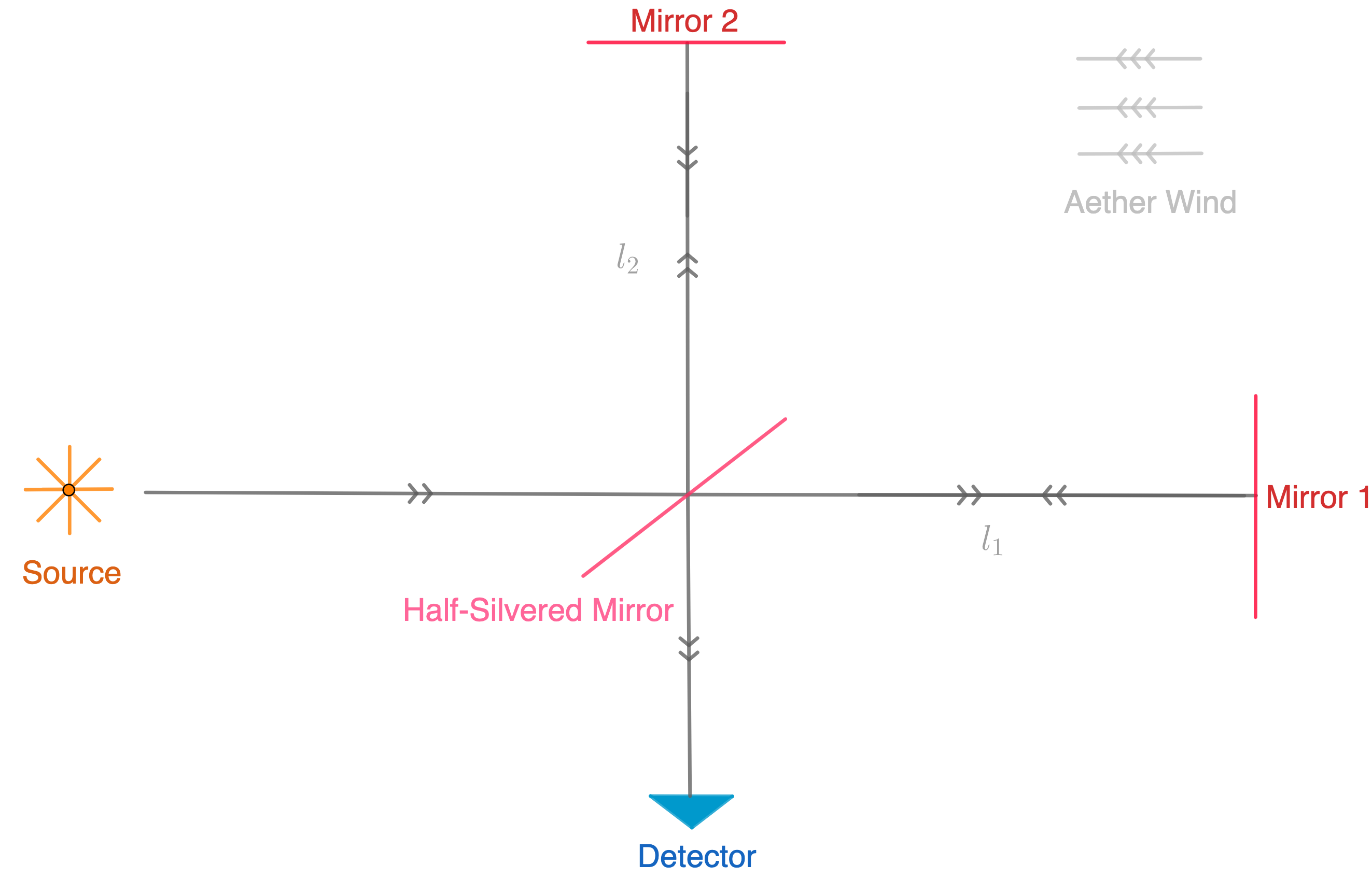
Suppose that the whole experiment is on the earth and the earth itself is among ether. The rotation of the earth cause of ether wind (assume with velocity v). The experiment was performed at different times of day and year. The speed of light relative to the source is c-v, and c is the speed of light. Then we can calculate the time that light is directed through and back from mirror one as below:

$t_1= \frac{l_1}{c-v}+\frac{l_1}{c+v}=\frac{2l_1}{c}\frac{1}{{1-\frac{v^2}{c^2}}}$

We can use the Maclaurin series as below for an approximation of this time. for $|x|<1$

$\frac{1}{1-x}=\displaystyle\sum_{n=0}^\infty x^n$

Then using this approximation and proportional velocity of orbiting of the earth around the sun to the light velocity:

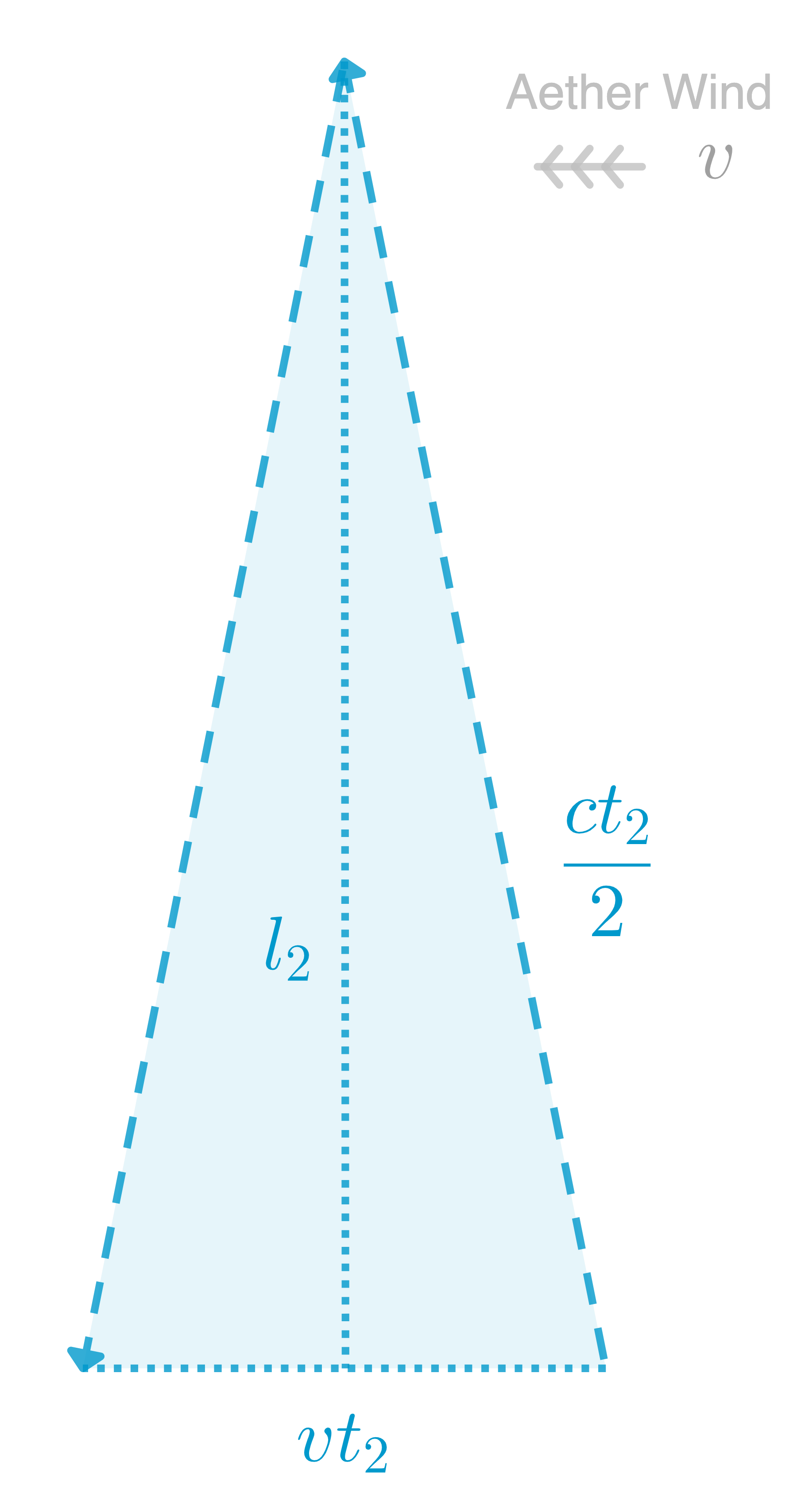
$\frac{v}{c} \approx 10^{-4} \Rightarrow t_1\approx \frac{2l_1}{c}({{1+\frac{v^2}{c^2}}})$

and for mirror 2 we have:

$l_2^2+(\frac{vt_2}{2})^2=(\frac{ct_2}{2})^2 \Rightarrow t_2= \frac{2l_2}{c}\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}$

According to Binomial Series, we can approximate the time as below:

$(1+x)^\alpha=\displaystyle\sum_{n=0}^\infty \binom{\alpha}{n} x^n \Rightarrow t_2\approx \frac{2l_2}{c}(1+\frac{v^2}{c^2})$

Now the rays recombine at the detector separated by

$\Delta t = t_2 - t_1 = \frac{2}{c}(l_2-l_1 + \frac{v^2}{c^2}(\frac{l_2}{2}-l_1))$

Suppose the apparatus is rotated 90 degrees, so that arm 1 is now transverse to the ether wind.

$\Delta t^\prime = t^\prime_2 - t^\prime_1 = \frac{2}{c}(l_2-l_1 + \frac{v^2}{c^2}({l_2}-\frac{l_1}{2}))$

Then the time change produced by rotating the apparatus is:

$\Delta t-\Delta t^\prime=\frac{v^2}{c^3}(l_1+l_2)$

The speed of light is constant and the same in all directions and in
all inertial frames.

In the Michelson-Morley experiment, a light beam was reflected several times backward and forwards to increase the difference in time between the two paths, and thus increase the sensitivity of the experiment. If the aether wind speed was comparable to the speed of the earth in orbit around the sun, Michelson calculated that a windspeed of just one or two miles a second would have observable effects in this experiment. However, no change in light intensity was observed, indicating that the aether did not exist.

To further test the existence of the aether, Michelson redesigned the experiment to use the earth’s daily rotation to detect an aether wind. In this version of the experiment, the interferometer was rotated so that one arm was parallel to the direction of the earth’s motion, and the other arm was perpendicular to it. If the aether existed, the speed of light would be affected differently in the two arms of the interferometer, leading to a measurable difference in the interference pattern. However, no such difference was observed, indicating that the aether did not exist.

As a final experiment, Michelson conducted the experiment on top of a high mountain in California to see if the aether stuck to the earth. If the aether was fixed to the earth, then the interferometer should have detected an aether wind due to the earth’s rotation. However, no such wind was observed, further supporting the conclusion that the concept of an all-pervading aether was incorrect from the beginning.

The null results of the Michelson-Morley experiment can be explained using the Lorentz-Fitzgerald contraction hypothesis and the special theory of relativity. According to these theories, the speed of light is constant and the same in all directions and in all inertial frames. This means that the observed null result of the Michelson-Morley experiment can be interpreted as evidence that the aether does not exist, and that the speed of light is independent of the motion of the observer.

Photoelectric effect

The first photovoltaic cell was invented by Edmond Becquerel in 1839. In this experiment, silver chloride or silver bromide was used to coat the platinum electrodes; once the electrodes were illuminated upon exposure to light, voltage and current were generated. The photovoltaic effect is closely related to the photoelectric effect.
In 1887, Heinrich Hertz Understood that with shining light on metal, an electron is ejected, and this phenomenon is known as the Photoelectric effect. The receiver in his apparatus consisted of a coil with a spark gap, where a spark would be seen upon detection of electromagnetic waves. The difference between photovoltaic and photoelectric is that in photoelectric, electrons are ejected out of the material into space or vacuum, but in photovoltaic, electrons enter the conduction bound of the material. The photovoltaic effect occurs more because it doesn’t require much energy that’s free electron from the material. Hertz discovered the effect by accident when he studied electromagnetic waves. After Hertz, Aleksandr Stoletov invented a new experimental setup and discovered direct proportionality between intensity of light and induced photoelectric current

The weirdness of this theory for the scientist of that period was that if the light is a wave, then these statements should pass:

The energy is distributed throughout the wavefront. Since the wavefront is spread over the metal surface, the energy is shared by all the electrons on the surface of the metal.
Decreasing intensity corresponds to supplying less energy per second to the electrons. Thus, electrons need more time to accumulate the energy required for emission.
Decreasing the intensity decreases the energy supplied to the electrons. Once the energy supplied is small enough, it stops the electrons from ejecting and thus stops the photoelectric emission.
increasing the intensity corresponds to supplying more energy per second to each electron on the surface of the metal; thus, the electrons eject at greater speeds. So, the average kinetic energy will increase.

But what they saw couldn’t explain the phenomena based on the wave theory of light. The first one is changing the intensity of light, and the second one is changing the frequency of it and checking the changes in kinetic energy and the number of electrons emitted. They saw that with increasing the intensity of light, there is no change in the kinetic energy of emitted electrons but instead an increase in the number of electrons emitted. They also understood with increasing(or decreasing) the frequency, the kinetic energy of the emitted electron increases(or decreases), and the number of emitted electrons does not change. The special thing about this experiment was that there was a critical frequency. If you take a sample and you irradiate it, it would begin with the light of very low frequency; nothing would happen, and after a certain frequency, you would get a current. Then there is a threshold frequency $\nu_0$ such that for $\nu>\nu_0$ there is current.
This $\nu_0$ depends on the metal and the configuration of atoms at the surface. Also, the magnitude of the current is proportional to the light intensity. The energy of photoelectrons is independent of the intensity of Lights.

In order to explain what was happening, it turned out that an entirely new model of light was needed. That model was developed by Albert Einstein. We will see the details of it in future sections.

Gas Discharge Tube & Cathode Ray

In 1838 Faraday applied a high voltage between two electrodes at either end of a glass tube that had been partially evacuated of air and noticed a strange light with its beginning at the Cathode (negative electrode ) and its end at the Anode.
Faraday noticed a dark space in front of Cathode. Pine Ridge Geisler Sucked even more, air and observed a glow filling the tube. By 1870 William Crookes evacuated the tube to lower pressure X atm. Crookes found that the Faraday dark space spread down the tube from Cathode toward Anode Until the tube became totally dark, but the glass of the tube at the end of it began to glow. The reason was that as more air was pumped out of the tube, fewer gas molecules obstructed the electron motion from the Cathode, so they traveled a longer distance, on average, before they stuck one, and they could travel in a straight line through the anode. The electrons are invisible, but when they hit the glass walls of the tube, they excite the atoms in the glass and make them give off fluorescence, usually yellow-green.
Johann Wilhelm Hittorf was first to recognize in 1869 that something must be traveling in straight lines from the Cathode to cast The Shadow, and in 1876, Eugen Goldstein proved that they came from the Cathode and named them cathode rays. Notice that at this time, we don’t know anything from something as an electron, and even we don’t know what carries electric currents. Crookes believed these are ‘radiant matter’ that is electrically charged atoms, and Hertz and Goldstein thought they were ether vibrations.

Suppose that we have a tube with $0.01 pa$ pressure. In 1897, Joseph John Thomson put a magnet beside the tube, and because the magnet affects moving charges, it deflects the ray. Although if we put charged plates on two sides of the tube, we can see that the ray deflects towards the positively charged plate, which means the ray consists of negatively charged particles; that is how J.J Thomson concluded.

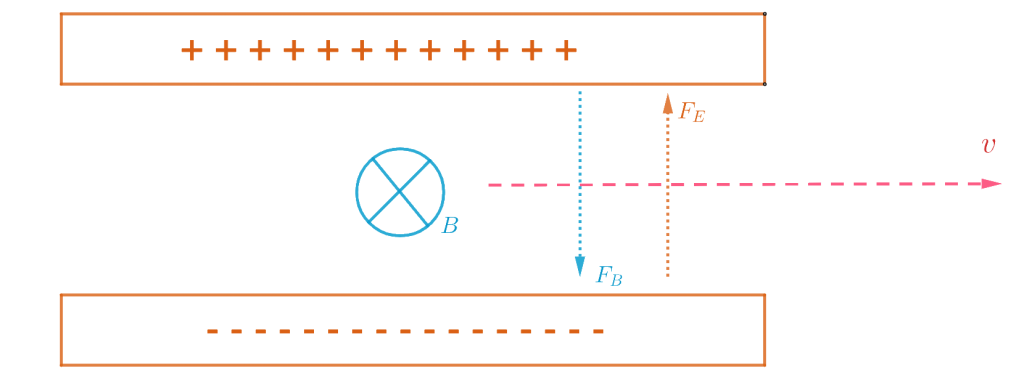
If we have negative and positively charged plates, then electrons accelerate toward the positive plate. It will also be another Force to repel it from negative plates.
A magnetic field causes the electron to change its direction. Not necessarily speed up but accelerate in a way that can cause it to change direction.
Suppose we have an electron toward $+x$ and magnetic field come in out of page $+y$ then electron feels a force to word $+z$ then dotted line is the path that electron go through it you can extend this to make a circle. J.J. could compute the proportional charge through the mass of the electron. The magnetic force on a moving charge can be computed as below

$F_B=qvB$

That $q$ is the charge, $v$ is velocity, and $B$ is the strength of the magnetic field. in this example magnetic force provides centripetal force $F_c=m\frac{v^2}{r}$ . we can set these two forces equal and obtain charge through the mass of the electron

$m\frac{v^2}{r}=qvB ⇒ \frac{v}{Br}=\frac{q}{m}$

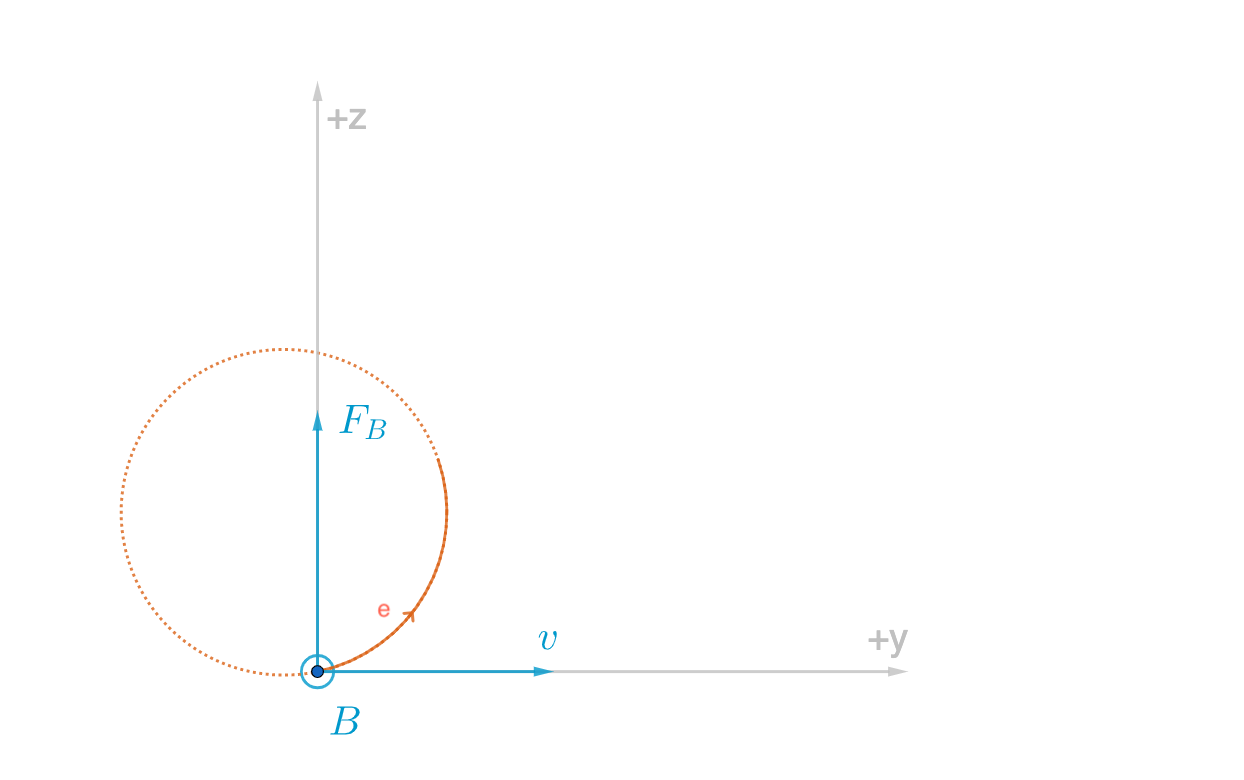
But in the experiment, it is not easy to find the velocity of the electron. Then by adding an electric field $F_E=qE$ equal to the magnetic field, we have

$qvB=qE ⇒ v=\frac{E}{B}$

and finally we have:

$\frac{q}{m}=\frac{E}{B^2r}$

By turning off the electric field, Thomson could measure the deflection of the cathode rays in the magnetic field alone, and the beam bent into a circular arc, and he measured the radius of this deflection. When repeating the experiment with different metals as electrode materials, Thomson found that the charge-to-mass ratio did not charge. The value was not affected by different gases in the tube or different metal electrodes.

J.J. concluded that $\frac{q}{m}=-1.76 \times 10^8 clg$ . Also, he realized that the cathode is composed of negatively charged particles, and these particles must exist as part of the atom because the mass of each particle is $≈ \frac{1}{1800}$ of the Hydrogen atom. He mentioned that these subatomic particles could be found within atoms of all elements. J.J. Knew that atoms have an overall neutral charge, and he introduced the “Plum Pudding Model of Atom” that atoms could be described as negative particles floating with a soup of diffuse positive charge.

Therefore, they were new particles, the first subatomic particle to be discovered, which he originally called “corpuscle” but was later named electron. Furthermore, he showed that these particles were identical to those released by photoelectric experiments. As a result of his work, Thomson won the Nobel Prize in Physics in 1906. His particles carry electric current in metal wires and carry the negative charge of an atom.

A Catastrophe Is Looming

The ultraviolet catastrophe was a problem in classical physics that arose in the late 19th century when attempting to calculate the total amount of energy radiated by a blackbody at all wavelengths. The problem was first identified by Gustav Kirchhoff in 1859, and later studied in detail by a number of prominent physicists in the late 19th and early 20th centuries.

One of the earliest attempts to calculate the spectral distribution of energy in a blackbody was made by Dulong and Petit in 1817. They assumed that the energy of radiation was proportional to the square of the amplitude of the oscillations of the electric field, and that the frequency of the radiation was proportional to the velocity of the oscillating charges. Using these assumptions, they derived a formula for the spectral radiance of a blackbody that was proportional to the square of the frequency of the radiation. However, their formula did not account for the variation of the frequency of the radiation with temperature, and did not accurately describe the experimental data.

Mathematically, the relationship between the transmittance ( $t_\lambda$ ), absorptance ( $a_\lambda$ ), and reflectance ( $r_\lambda$ ) of a material can be expressed as:

$t_\lambda+a_\lambda+r_\lambda=1$

This equation indicates that the total amount of radiation that interacts with a material must either be transmitted, absorbed, or reflected, with no radiation lost or gained in the process. In the case of a black body, the absorptance is unity ( $a_\lambda=1$ ), meaning that all radiation incident upon the object is absorbed and converted into thermal energy, which is then re-emitted as black body radiation.

There are some similarities between blackbody radiation and an ideal gas, as both are physical systems that exhibit certain behaviors and properties. One similarity is that both blackbody radiation and an ideal gas have particles (photons in the case of blackbody radiation, and gas molecules in the case of an ideal gas) that move in all directions with a range of velocities. This random motion leads to properties such as pressure and energy density. Another similarity is that both blackbody radiation and an ideal gas exert pressure on the walls of their container. In the case of an ideal gas, this is due to the collisions of gas molecules with the walls of the container, while in the case of blackbody radiation, the pressure is due to the transfer of momentum from photons to the walls of the container. Additionally, both blackbody radiation and an ideal gas have energy density. In the case of an ideal gas, the energy density is related to the temperature of the gas, while in the case of blackbody radiation, the energy density is related to the intensity of the radiation and the frequency of the photons.

However, there are also significant differences between blackbody radiation and an ideal gas. For example, blackbody radiation consists of electromagnetic waves, while an ideal gas consists of particles. Additionally, the energy of blackbody radiation is continuous and can take any value, while the energy of an ideal gas is quantized.

Pierre Prévost’s paper, “Essai sur le feu” (Essay on Heat), published in 1791, proposed the notion of radiation in a systematic method, which is now known as the theory of exchange. The theory of exchange describes the exchange of radiation between two bodies in thermal equilibrium, and states that two bodies in thermal equilibrium exchange radiation at equal rates regardless of the emissivities of the surfaces.

Mathematically, Prévost’s theory of exchange can be expressed as:

$\frac{dQ_1}{dt} = \frac{dQ_2}{dt}$

where $dQ_1$ and $dQ_2$ are the rates of exchange of radiation between the two bodies. This equation states that the rates of exchange of radiation are equal, and that the net heat transfer between the two bodies is zero.

Physically, Prévost’s theory of exchange is based on the principle of conservation of energy. Prévost proposed that a body emits radiation because of the motion of its particles, and that the energy of the emitted radiation is equal to the kinetic energy of the particles. He further proposed that when two bodies are in thermal equilibrium, the rate of emission of radiation by each body is equal to the rate of absorption of radiation from the other body, so that the net exchange of energy between the two bodies is zero.

Prévost’s theory of exchange is important in the study of blackbody radiation, and is a precursor to the more complete description of blackbody radiation provided by the Stefan-Boltzmann law and Planck’s law. The theory of exchange also has applications in other areas of physics, such as the study of heat transfer and thermodynamics.

Gustav Kirchhoff’s paper “On the relation between the radiating and absorbing powers of different bodies for light and heat” published in 1860, is a seminal work in the study of radiation and thermodynamics. In this paper, Kirchhoff derived the law that is now known as Kirchhoff’s law, which states that at thermal equilibrium, the ratio of the spectral emissivity of a blackbody to its spectral absorptivity is equal to the Planck radiation intensity at that wavelength and temperature.

Mathematically, Kirchhoff derived this law by considering a blackbody at temperature $T$ that is in thermal equilibrium with its surroundings. He assumed that the radiative exchange between the blackbody and its surroundings was in a steady state, so that the rate of energy absorbed by the blackbody per unit time and area was equal to the rate of energy emitted by the blackbody per unit time and area.

Kirchhoff then considered an infinitesimal layer of thickness $dx$ within the blackbody, at a distance $x$ from the surface. He assumed that the spectral emissivity and absorptivity of the layer were $e_\lambda(x)$ and $a_\lambda(x)$ , respectively, at wavelength $\lambda$ . Kirchhoff applied the principle of detailed balance to this layer, which states that the rate of absorption of energy by the layer at wavelength $\lambda$ must equal the rate of emission of energy by the layer at the same wavelength. Mathematically, this can be expressed as:

$a_\lambda(x)B_\lambda(T) = e_\lambda(x)B_\lambda(T)$

where $B_\lambda(T)$ is the Planck radiation intensity at temperature $T$ and wavelength $\lambda$ . Kirchhoff then integrated this equation over all wavelengths from 0 to $\infty$ to obtain:

$\int_0^\infty a_\lambda(x)B_\lambda(T)\,d\lambda = \int_0^\infty e_\lambda(x)B_\lambda(T)\,d\lambda$

which can be rearranged to give:

$\frac{\int_0^\infty e_\lambda(x)B_\lambda(T)\,d\lambda}{\int_0^\infty a_\lambda(x)B_\lambda(T)\,d\lambda} = 1$

This is Kirchhoff’s law, which states that at thermal equilibrium, the ratio of the spectral emissivity of a blackbody to its spectral absorptivity is equal to the Planck radiation intensity at that wavelength and temperature.

Kirchhoff’s law has important applications in the study of blackbody radiation, and is a precursor to the more complete description of blackbody radiation provided by the Stefan-Boltzmann law and Planck’s law. Kirchhoff’s law also has applications in other areas of physics, such as the study of radiative transfer and atmospheric science.

In 1879, Josef Stefan and Ludwig Boltzmann independently derived the Stefan-Boltzmann law, which describes the total power radiated per unit area by a blackbody as a function of its temperature. The law is given by:

$\Phi = \sigma T^4$

where $\Phi$ is the total power radiated per unit area by a blackbody, $T$ is the absolute temperature of the blackbody, and $\sigma$ is the Stefan-Boltzmann constant, which has a value of approximately $5.67 \times 10^{-8}$ watts per square meter per Kelvin to the fourth power.

The Stefan-Boltzmann law can be derived from the Planck radiation law, which gives the spectral radiance of a blackbody as a function of its temperature and wavelength. The Planck radiation law is given by:

$B_{\lambda}(T) = \frac{2hc^2}{\lambda^5} \frac{1}{e^{\frac{hc}{\lambda k_B T}} - 1}$

where $B_{\lambda}(T)$ is the spectral radiance of the blackbody at wavelength $\lambda$ and temperature $T$ , $h$ is Planck’s constant, $c$ is the speed of light, and $k_B$ is Boltzmann’s constant.

To obtain the Stefan-Boltzmann law, we integrate the Planck radiation law over all wavelengths from 0 to $\infty$ to obtain the total radiative power per unit area:

$\Phi = \int_{0}^{\infty} B_{\lambda}(T) d\lambda$

Substituting the Planck radiation law into this expression and performing the integration yields:

$\Phi = \frac{2\pi^5 k_B^4}{15c^2h^3} T^4$

This expression can be simplified using the definition of the Stefan-Boltzmann constant $\sigma = \frac{2\pi^5 k_B^4}{15c^2h^3}$ , giving:

$\Phi = \sigma T^4$

This is the Stefan-Boltzmann law.

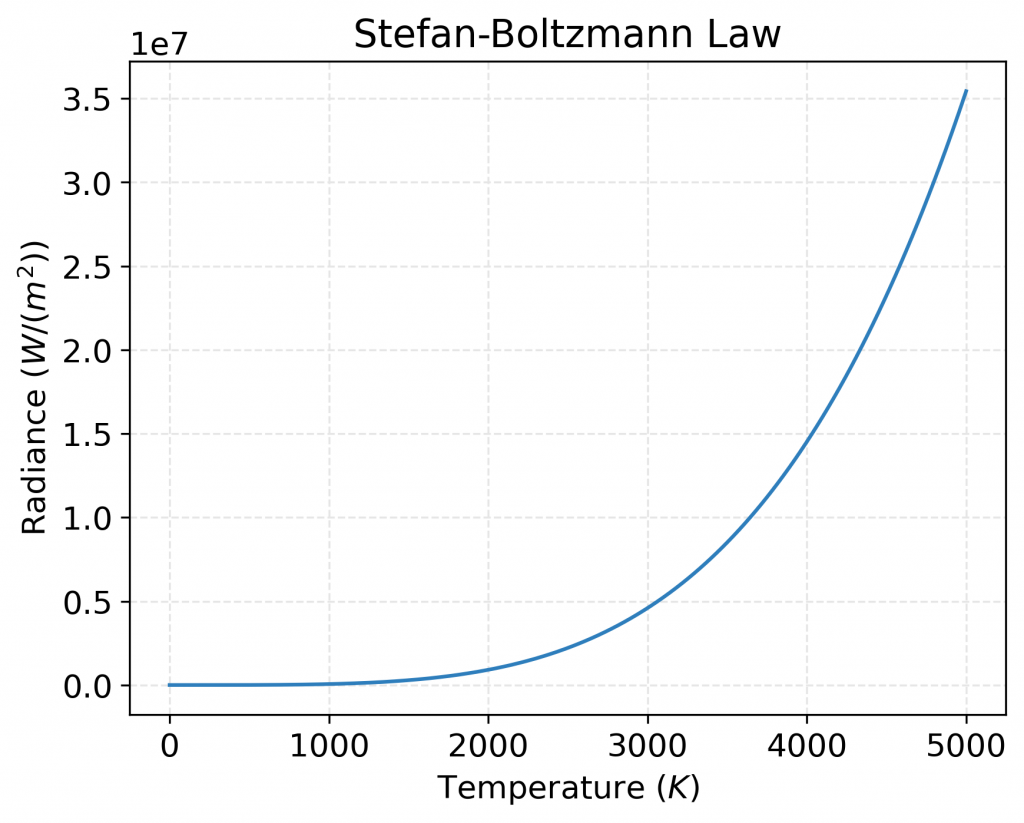
Plot of radiance values predicted by the Stefan-Boltzmann law as a function of temperature. The plot shows how the radiance emitted by a black body increases rapidly as the temperature increases, in accordance with the fourth power law. The cyan curve represents the radiance values over a range of temperatures from 0.1 K to 5000 K.

Physically, the Stefan-Boltzmann law describes the total power radiated per unit area by a blackbody as a function of its temperature. The law is a consequence of the fact that a blackbody is a perfect absorber and emitter of radiation at all wavelengths. The law has important applications in a variety of fields, including astronomy, atmospheric science, and engineering.

In Boltzmann’s derivation of the Stefan-Boltzmann law, he used an empirical formula for the spectral radiance of a blackbody that was based on experimental measurements. This formula, which was derived by Wien and Rayleigh in the 1890s, did not explicitly involve the Planck constant. Instead, it was based on the assumption that the radiation emitted by a blackbody could be treated as a gas of independent harmonic oscillators, each with a characteristic frequency and energy.

Later, when Planck introduced his theory of blackbody radiation in 1900, he used Boltzmann’s statistical mechanics to derive the Planck radiation law, which did involve the Planck constant. Planck’s theory explained the quantization of energy in the radiation emitted by a blackbody and provided a theoretical basis for the empirical formula used by Wien and Rayleigh.

The Rayleigh-Jeans law is an empirical formula that describes the spectral radiance of electromagnetic radiation emitted by a blackbody at a given temperature. The law was proposed independently by Lord Rayleigh and Sir James Jeans in the late 19th and early 20th centuries, before the development of quantum mechanics and the Planck radiation law.

The Rayleigh-Jeans law is based on the classical theory of electromagnetic radiation, which treats the radiation as a collection of classical oscillators. According to this theory, the spectral radiance of a blackbody is proportional to the product of the temperature and the fourth power of the wavelength. Mathematically, the Rayleigh-Jeans law is given by:

$B_{\lambda}(T) = \frac{2ck_B T}{\lambda^4}$

where $B_{\lambda}(T)$ is the spectral radiance of the blackbody at wavelength $\lambda$ and temperature $T$ , $k_B$ is Boltzmann’s constant, $c$ is the speed of light, and $\lambda$ is the wavelength of the radiation.

The Rayleigh-Jeans law was successful in predicting the behavior of blackbody radiation at long wavelengths, but it failed at short wavelengths, where it predicted an infinite amount of energy. This problem, known as the ultraviolet catastrophe, was one of the key problems that led to the development of quantum mechanics and the Planck radiation law.

Max Planck proposed in 1900 that the energy of electromagnetic radiation was quantized, meaning that it could only take on certain discrete values. This led to a new formula for the spectral radiance of a blackbody, known as the Planck radiation law, which successfully explained the behavior of blackbody radiation at all wavelengths. Planck’s theory was based on the assumption that the radiation was emitted and absorbed in discrete packets of energy, or quanta, with the energy of each quantum given by $E = hf$ , where $h$ is Planck’s constant and $f$ is the frequency of the radiation.

To derive the Rayleigh-Jeans law, Lord Rayleigh and Sir James Jeans began with the classical theory of electromagnetic radiation, and assumed that the radiation was emitted by a large number of independent oscillators with a range of frequencies. They then used statistical mechanics to calculate the average energy of each oscillator at a given temperature, and integrated over all frequencies to obtain the total energy density of the radiation. The result was:

$u(\lambda, T) = \frac{8\pi k_B T}{\lambda^4}$

where $u(\lambda, T)$ is the energy density of the radiation at wavelength $\lambda$ and temperature $T$ , $k_B$ is Boltzmann’s constant, and $\lambda$ is the wavelength of the radiation.

From this expression, the spectral radiance can be obtained by dividing by the speed of light and multiplying by $\pi$ :

$B_{\lambda}(T) = \frac{2ck_B T}{\lambda^4}$

This is the Rayleigh-Jeans law.

Max Planck’s paper on blackbody radiation, titled “On the Law of Distribution of Energy in the Normal Spectrum,” was published in 1901 in the journal Annalen der Physik. In this paper, Planck proposed a new theory of blackbody radiation based on the assumption that the energy of electromagnetic radiation was quantized, or could only take on certain discrete values.

Planck began his derivation by assuming that the energy of an oscillator that emits radiation at frequency $f$ is quantized, with the energy of each quantum given by $E = hf$ , where $h$ is Planck’s constant. He also assumed that the oscillator could only emit or absorb energy in whole quanta, meaning that the energy of the oscillator could only change by an integer multiple of $hf$ .

Planck then considered a large number of such oscillators with different frequencies, and derived an expression for the amount of energy that each oscillator would emit in thermal equilibrium at a given temperature $T$ . This expression was:

$\frac{8\pi hf^3}{c^3} \frac{1}{e^{\frac{hf}{k_BT}} - 1}$

where $h$ is Planck’s constant, $f$ is the frequency of the radiation, $c$ is the speed of light, $k_B$ is Boltzmann’s constant, and $T$ is the temperature.

Planck then integrated this expression over all frequencies to obtain the total energy density of the radiation. The result was:

$u(\lambda, T) = \frac{8\pi hc}{\lambda^5} \frac{1}{e^{\frac{hc}{\lambda k_BT}} - 1}$

where $u(\lambda, T)$ is the energy density of the radiation at wavelength $\lambda$ and temperature $T$ , $h$ is Planck’s constant, $c$ is the speed of light, $k_B$ is Boltzmann’s constant, and $\lambda$ is the wavelength of the radiation.

From this expression, Planck was able to derive the spectral radiance of a blackbody, which is the energy radiated by the blackbody per unit time, per unit area, per unit solid angle, and per unit wavelength. The spectral radiance is given by:

$B_{\lambda}(T) = \frac{2hc^2}{\lambda^5} \frac{1}{e^{\frac{hc}{\lambda k_BT}} - 1}$

The Planck radiation law successfully explained the behaviour of blackbody radiation at all wavelengths, including the short wavelengths where the Rayleigh-Jeans law predicted an infinite amount of energy. It also provided a theoretical basis for Wien’s empirical law, which had been successful in describing the shape of the blackbody radiation curve at short wavelengths.

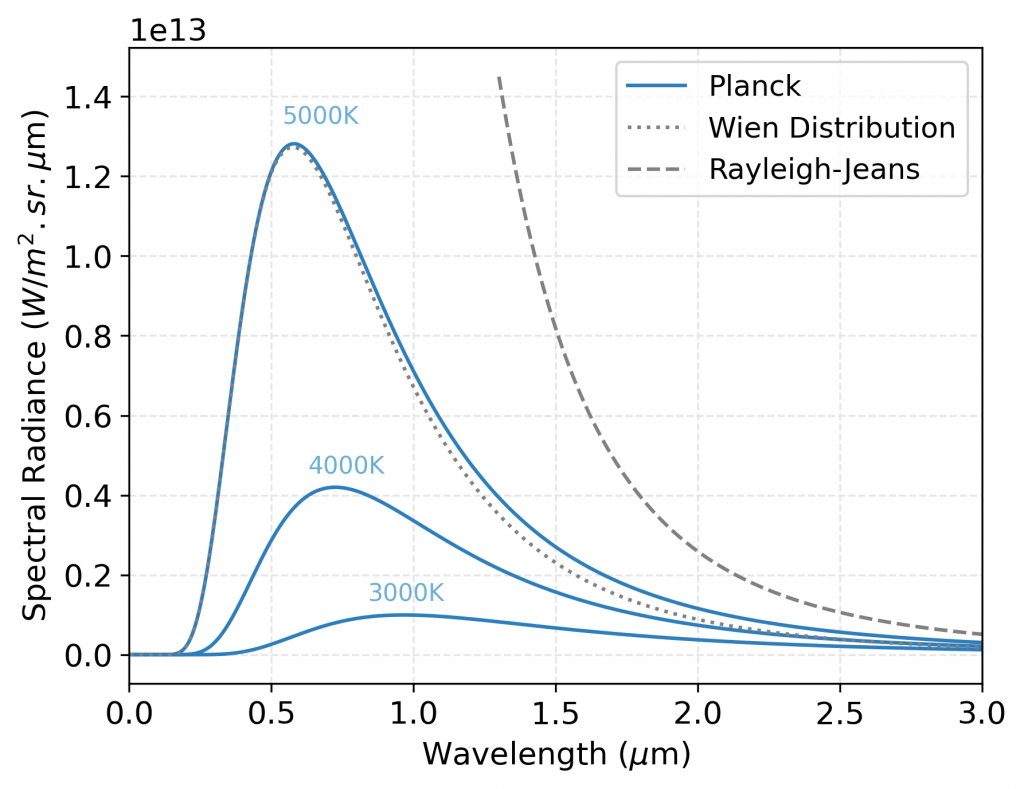
Comparison of the spectral radiance distributions for a black body at a temperature of 5000 K using three different approaches: Rayleigh-Jeans formula (dashed gray line), Planck’s law (solid blue line), and Wien’s distribution (dotted gray line). The plot shows that the Rayleigh-Jeans formula overestimates the spectral radiance at shorter wavelengths, while the Wien distribution underestimates it at longer wavelengths. Planck’s law provides a more accurate description of the spectral radiance, with a characteristic peak that shifts to shorter wavelengths and increases in height as the temperature increases. The plot also includes a legend for the different approaches.

The ultraviolet catastrophe was a problem in classical physics that arose when attempting to calculate the total energy radiated by a blackbody at all wavelengths. According to the classical theory of electromagnetic radiation, the total energy radiated per unit area per unit time should be infinite, since the spectral radiance predicted by the Rayleigh-Jeans law increases without limit as the wavelength decreases.

Max Planck’s solution to the ultraviolet catastrophe was to introduce the concept of energy quantization, which is a fundamental principle of quantum mechanics. In his theory, Planck assumed that the energy of electromagnetic radiation was quantized, meaning that it could only take on certain discrete values. This was a departure from classical physics, which assumed that energy could take on any continuous value.

By assuming energy quantization, Planck was able to derive a new formula for the spectral radiance of a blackbody that successfully explained the behavior of blackbody radiation at all wavelengths. The formula, known as the Planck radiation law, includes a factor of $e^{\frac{hc}{\lambda k_B T}}$ in the denominator, which accounts for the quantization of energy. This factor causes the spectral radiance to decrease exponentially at short wavelengths, preventing it from increasing without limit as predicted by the Rayleigh-Jeans law.

Thus, by introducing the concept of energy quantization, Planck was able to solve the ultraviolet catastrophe and provide a theoretical explanation for the observed behavior of blackbody radiation. His theory marked a major milestone in the development of quantum mechanics and had profound implications for our understanding of the behavior of matter and energy at the atomic and subatomic level.

Bibliography

Bohr, N. (n.d.). On the Constitution of Atoms and Molecules. 24.
Branchetti, L., Cattabriga, A., & Levrini, O. (2019). Interplay between mathematics and physics to catch the nature of a scientific breakthrough: The case of the blackbody. Physical Review Physics Education Research, 15(2), 020130. https://doi.org/10.1103/PhysRevPhysEducRes.15.020130
Buchwald, J. Z. (1989). The battle between Arago and Biot over Fresnel. Journal of Optics, 20(3), 109–117. https://doi.org/10.1088/0150-536X/20/3/002
Darrigol, O. (2012a). A History of Optics from Greek Antiquity to the Nineteenth Century.
Darrigol, O. (2012b). A History of Optics from Greek Antiquity to the Nineteenth Century. OUP Oxford.
Fresnel, A.-J., & Putland, G. R. (tr. /ed. ). (2021). Memoir on the double refraction that light rays undergo in traversing the needles of quartz in the directions parallel to the axis. https://doi.org/10.5281/zenodo.5070327
Huygens, C. (1912). Treatise On Light. Macmillan And Company., Limited. http://archive.org/details/treatiseonlight031310mbp
I.—An Account of some Experiments on Radiant Heat, involving an extension of Prevost’s Theory of Exchanges | Earth and Environmental Science Transactions of The Royal Society of Edinburgh | Cambridge Core. (n.d.). Retrieved 16 July 2022, from https://www.cambridge.org/core/journals/earth-and-environmental-science-transactions-of-royal-society-of-edinburgh/article/abs/ian-account-of-some-experiments-on-radiant-heat-involving-an-extension-of-prevosts-theory-of-exchanges/8CC0C2ABFF8ADCE57DE899865A81FFDB
II. The Bakerian Lecture. On the theory of light and colours. (1802). Philosophical Transactions of the Royal Society of London, 92, 12–48. https://doi.org/10.1098/rstl.1802.0004
Mason, P. (1981). The Light Fantastic. Penguin.
Maxwell, J. C. (1831-1879) A. du texte. (1873). A treatise on electricity and magnetism. Vol. 2 / by James Clerk Maxwell,…https://gallica.bnf.fr/ark:/12148/bpt6k95176j
Pais, A. (1979). Einstein and the quantum theory. Reviews of Modern Physics, 51(4), 863–914. https://doi.org/10.1103/RevModPhys.51.863
Planck, M. (n.d.). On the Law of Distribution of Energy in the Normal Spectrum. 7.
Planck, M. (1967). On the Theory of the Energy Distribution Law of the Normal Spectrum. In The Old Quantum Theory (pp. 82–90). Elsevier. https://doi.org/10.1016/B978-0-08-012102-4.50013-9
RAYLEIGH. (1921). Young’s Interference Experiment. Nature, 107(2688), 298–298. https://doi.org/10.1038/107298a0
Rothman, T. (2003). Everything’s relative: And other fables from science and technology. Hoboken, N.J. : Wiley. http://archive.org/details/everythingsrelat0000roth
Society (London), R. (1670). Philosophical Transactions of the Royal Society of London: Giving Some Accounts of the Present Undertakings, Studies, and Labours, of the Ingenious, in Many Considerable Parts of the World.
Young’s Interference Experiment | Nature. (n.d.). Retrieved 16 July 2022, from https://www.nature.com/articles/107298a0
Zubairy, M. S. (2016). A Very Brief History of Light. In M. D. Al-Amri, M. El-Gomati, & M. S. Zubairy (Eds.), Optics in Our Time (pp. 3–24). Springer International Publishing. https://doi.org/10.1007/978-3-319-31903-2_1

Cite This Page

BibTeX

Page name: Corpuscule or Wave
Author: Arman Kashef
Publisher: Xaporia, The Free and Independent Blog
Date of last revision: 29 September 2022 05:13 UTC
Date retrieved: 5 June 2022 08:42 UTC
Permanent link: https://xaporia.com/quanta/light-corpuscule-or-wave
Page Version ID: 05062204cow

@misc{ 
        xaporia:05062204cow,
        author = "{Arman Kashef}",
        title = "Corpuscule or Wave --- {Xaporia}{,} The Free and Independent Blog",
        year = "2022",
        url = "https://xaporia.com/quanta/light-corpuscule-or-wave",
        note = "[Online; accessed 5-June-2022]"
      }

Spotlights

Ether, Light, Photoelectric, Polarization, Ultraviolet Catastrophe

Posted by:

Xaporia

4 responses to “Corpuscule or Wave”

Unknown

June 23, 2023 at 6:43 pm

Thanks for another excellent article. The place else
may just anybody get that kind of info in such an ideal manner of writing?
I’ve a presentation subsequent week, and I am at the look for such information.

Reply
Unknown

October 1, 2023 at 5:36 am

I am genuinely delighted to glance at this web site posts which carries lots
of valuable data, thanks for providing such information.

Reply
במרכז

November 17, 2023 at 5:45 am

I need to to thank you for this very good read!! I absolutely enjoyed every bit of it. I have got you book-marked to check out new stuff you postÖ

Reply
Unknown

November 29, 2023 at 5:25 pm

Very nice post. I just stumbled upon your weblog and wanted to say that
I have really enjoyed browsing it. After all I will be subscribing to your feed and I hope you write again soon!

Reply